变换(模型、视图、投影)
变换(模型、视图、投影)
1 观测(Viewing)变换
- 观测(Viewing)变换
- 视图(View)/ 相机(Camera)变换
- 投影(Projection)变换
- 正交(Orthographic)投影
- 透视(Perspective)投影
计算机图形学就是在做M(Model)V(View)P(Projection)变换,可以用现实中的拍照来类比:
- 找个好地方,安排好每个人的位置(模型变换,从局部空间到世界空间)
- 把相机放到一个好的角度(视图变换,从世界空间到观察空间)
- 按快门拍照(投影变换,从观察空间到裁剪空间)
对于 MVP 变换可以参考图形学:MVP变换概述
1.1 视图(View)/ 相机(Camera)变换
相机的定义:
- 相机的位置 ——
- 相机看向的方向 ——
- 相机朝上的方向 ——
默认相机的位置 在原点 (0, 0, 0),相机看向的方向 为 -Z,相机朝上的方向 为 Y,因此当相机不在原点时,需要先将相机摆到默认的位置,同时模型也随着相机同步移动
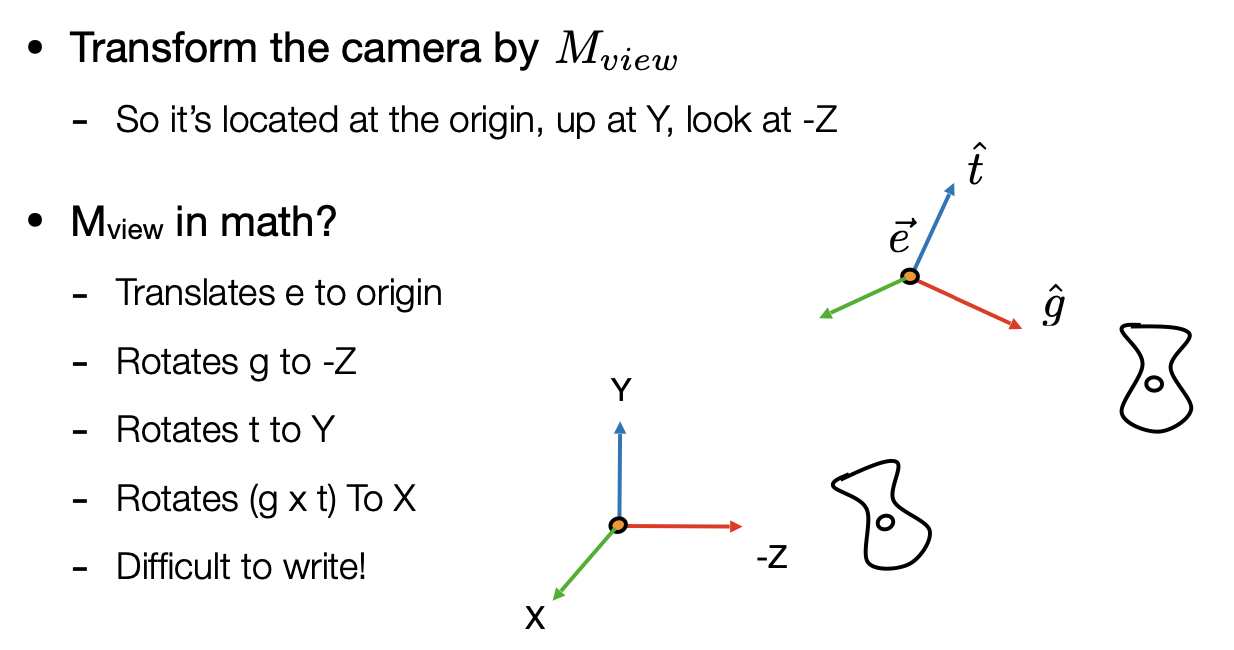
可以用 来表示,其中 表示平移变换 表示旋转变换,先将相机平移到原点, 很容易就能求出来, 很难直接求出,但是将默认位置旋转到相机的位置相对比较容易,因此可以先求出 (即默认位置旋转到相机的位置的旋转变换矩阵),又因为旋转变换的矩阵是正交矩阵,因此再将求出的矩阵进行转置就可以得到最后的

1.2 投影(Projection)变换
把三维的场景变成观测到的二维的图像,这就是投影。投影分为正交投影和透视投影。其中透视投影跟我们平时人眼观测到的成像差不多,近大远小。正交投影就是不发生近大远小的变化,几何上来说就是,正交投影中平行的线成像后依旧平行。
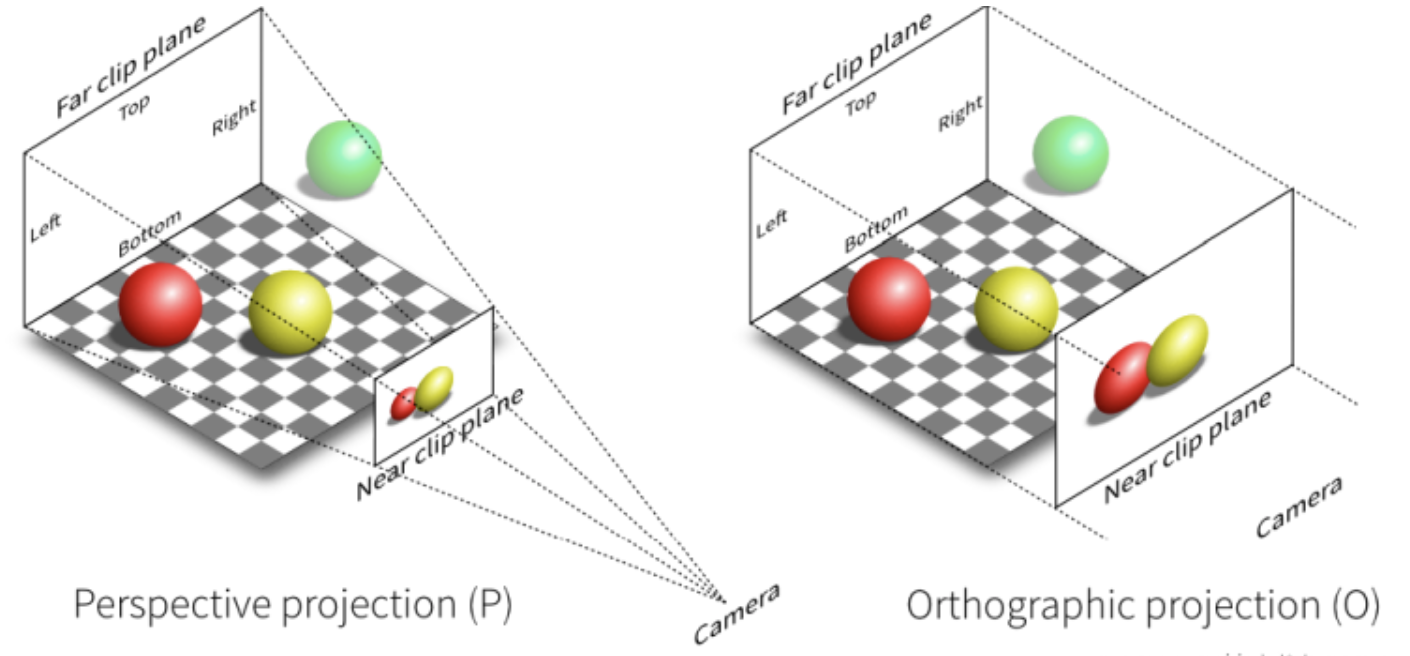
1.2.1 正交(Orthographic)投影
当可观测区域是一个 [l(eft), r(right)] * [b(ottom), t(op)] * [f(ar), n(ear)] 的长方体时,要让他变成 且中心在原点的标准(canonical)视体(默认要把可观测区域变成这样的立方体)
- 将长方体的中心平移到原点,中心坐标为
- 将各边放缩到长度为 2
其正交投影矩阵如下(此时物体肯定会被拉伸,之后的视口变换(5.2)操作中会恢复)
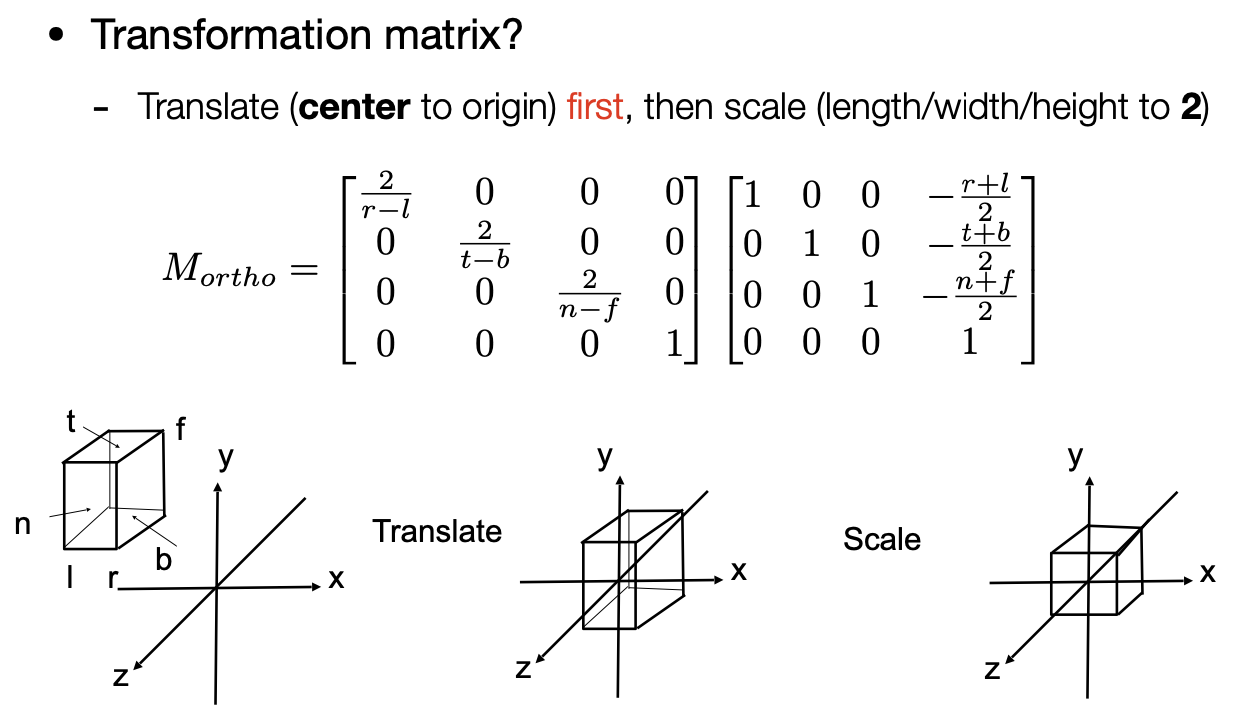
因为使用右手螺旋定则,所以看的方向是 -z,因此 far 会小于 near
1.2.2 透视(Perspective)投影
先将锥体中远平面到近平面之间的所有平面挤压到近平面的大小,使锥体变成长方体的样子

然后再利用正交投影的办法,因此透视投影的矩阵 ,,具体推导过程看视频。在锥体变为长方体的过程中,每个点的 z 分量会变小。从锥体变为长方体的过程可以理解为将 n 到 f 平面划分为无数个小平面,再将每个平面压缩成 n 平面的大小。对于下图可以假设以枕木为边界划分平面,枕木之间的距离就是两个平面之间的距离,在锥体中每个枕木之间的距离是相等的,而压缩到长方体时,就变得近大远小,可以近似理解为下图就是长方体中的样子。n 平面和 f 平面的 z 坐标都是不变的,而离镜头越远,枕木之间的距离越小,只能是每段枕木向远离镜头的方向移动,离镜头越远,z 越小。

对于透视投影可以参考图形学:正交/透视投影矩阵的推导(多个思路)
2 总结
Model 变换是从局部空间 (Local Space) 到 世界空间 (World Space);View 变换是从世界空间到观察空间 (View Space);Projection 变换是从观察空间到裁剪空间 (Clip Space);透视除法 (Perspective Division) 是从裁剪空间到标准设备坐标系 (Normalized Device Coordinate, NDC),这个变换通常是由硬件渲染管线自动进行;Viewport 变换是从 NDC 到屏幕空间 (Screen Space)。
