回顾线性代数
...约 404 字大约 1 分钟
回顾线性代数
1 向量的点乘
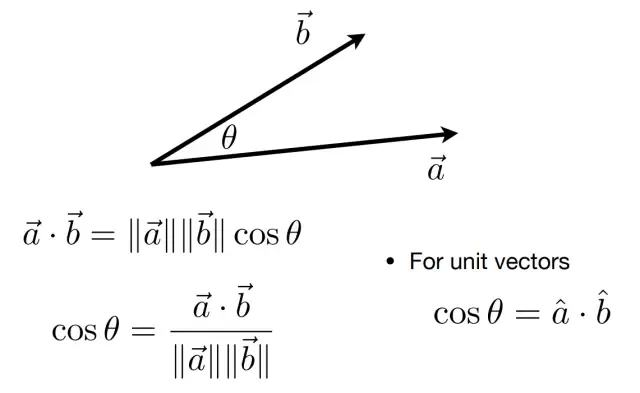
应用:
- 判断两个向量在方向上多么接近:向量的点积与它们夹角的余弦成正比,因此在聚光灯的效果计算中,可以根据点积来得到光照效果,如果点积越大,说明夹角越小,则物体离光照的轴线越近,光照越强。
- 分解一个向量
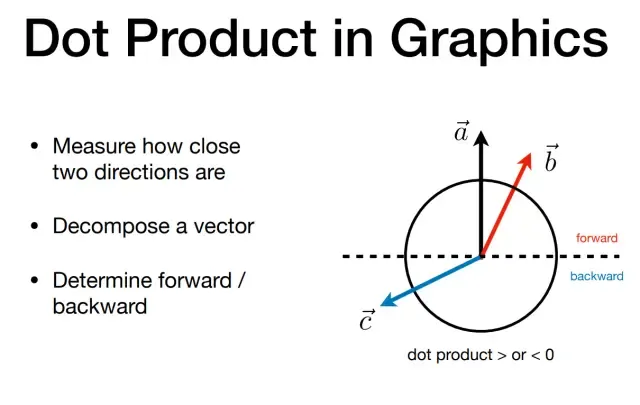
- 判断向量的方向性:
- 点乘为 0 表示两个向量垂直
- 点乘为正数表示两个向量方向基本一致
- 点乘为负数表示两个向量方向基本相反
2 向量的叉乘
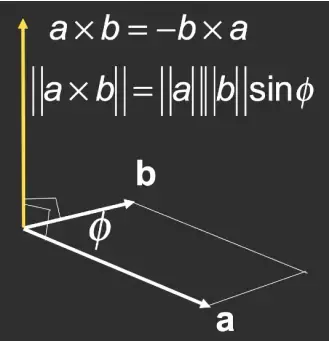
叉乘的结果是一个同时垂直于这两个向量的向量(两个相同的向量叉乘的结果是零向量),通过右手螺旋定则判断叉乘的结果的方向,如 a×b=c 四指从 a 的方向向 b 的方向握紧,大拇指指向的就是 c 的方向 。
应用:

- 判断两个向量的左右:a×b 得到结果是和 z 轴同向,是正的,说明 b 在 a 的左侧
- 判断一个点是否在三角形内部(做光栅化,给三角形内部像素着色需要用到):
- AB×AP > 0 说明 P 在 AB 左侧
- BC×BP > 0 说明 P 在 BC 左侧
- CA×CP > 0 说明 P 在 CA 左侧
- 因此说明 P 落在三角形 ABC 内部
3 点乘和叉乘的矩阵形式

Powered by Waline v2.15.5
