光栅化(抗锯齿与深度测试)
光栅化(抗锯齿与深度测试)
1 采样产生的问题
Sampling Artifacts in CG:(这里的 Artifacts 是指一切看上去不太对的东西,可以翻译为瑕疵)
- 锯齿(阶梯形状)
- 摩尔纹
- 车轮效应
- ...
产生 Artifacts 的原因:信号变化的太快了(频率太高),但是采样速率太慢
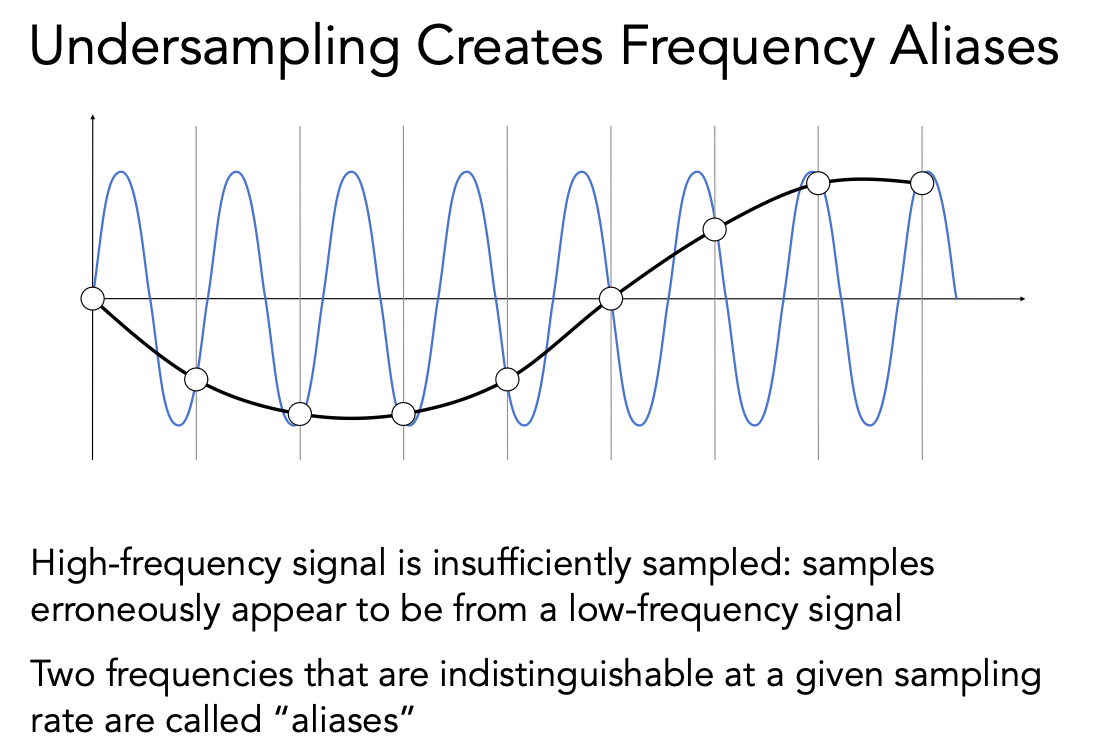
2 走样
对两个不同的函数进行采样,采样的结果完全相同,这就被称为走样(Aliases)
3 滤波
滤波(Filtering)就是去掉一些特定的频率
傅里叶变换可以把一个函数从时域(自变量是时间,因变量是信号的变化)变为频域(自变量是频率,因变量是该频率信号的幅度)
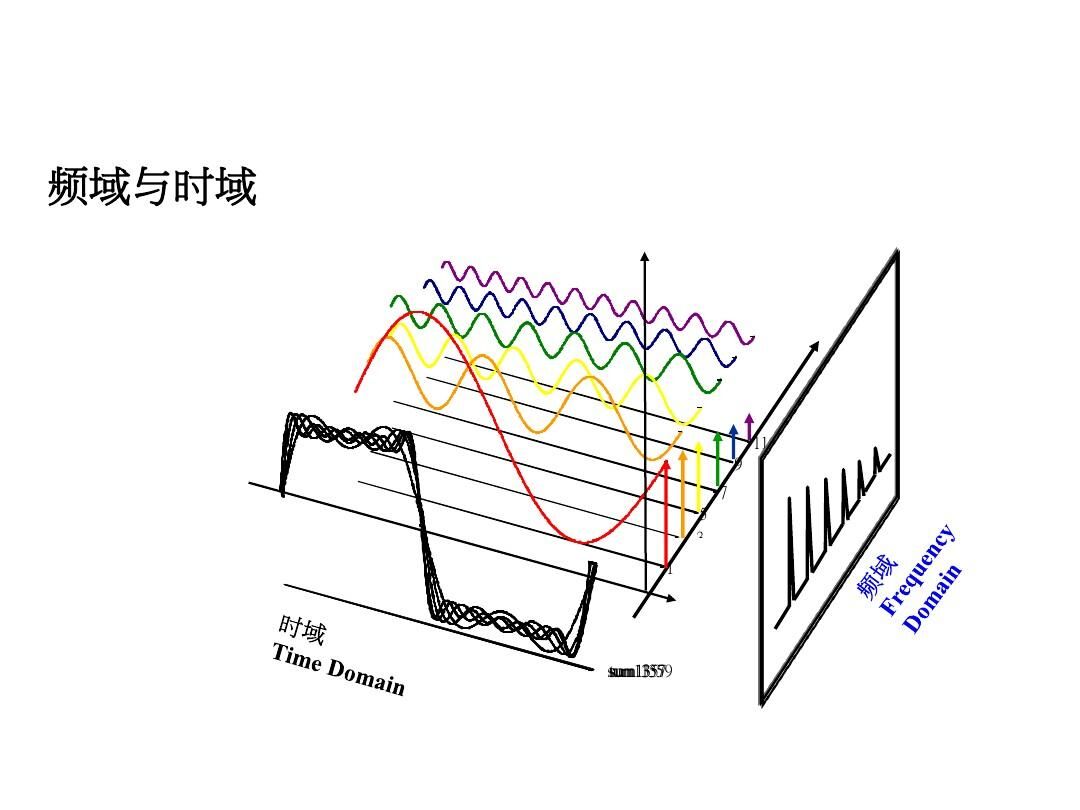
下图中,左图经过傅里叶变换可以变为右图(图像本身不带有时间信息,但空间上的位置也称为时域),右图是频谱图。在频谱图中,中间部分是低频信息,越往外越高频,亮度表示该频率信号的多少,越亮越多。

频谱图的水平和垂直方向会有两根很亮的线,因为在分析一个信号时,会认为它是一个周期性重复的信号,但是图像并没有这种特征,因此会认为图片到达边界后又会重复,即在水平方向和竖直方向上有无数张同样的图片,在图片的边界上会产生剧烈的变化,因此会产生极其高的高频,分析图片时可以忽略这两条线。
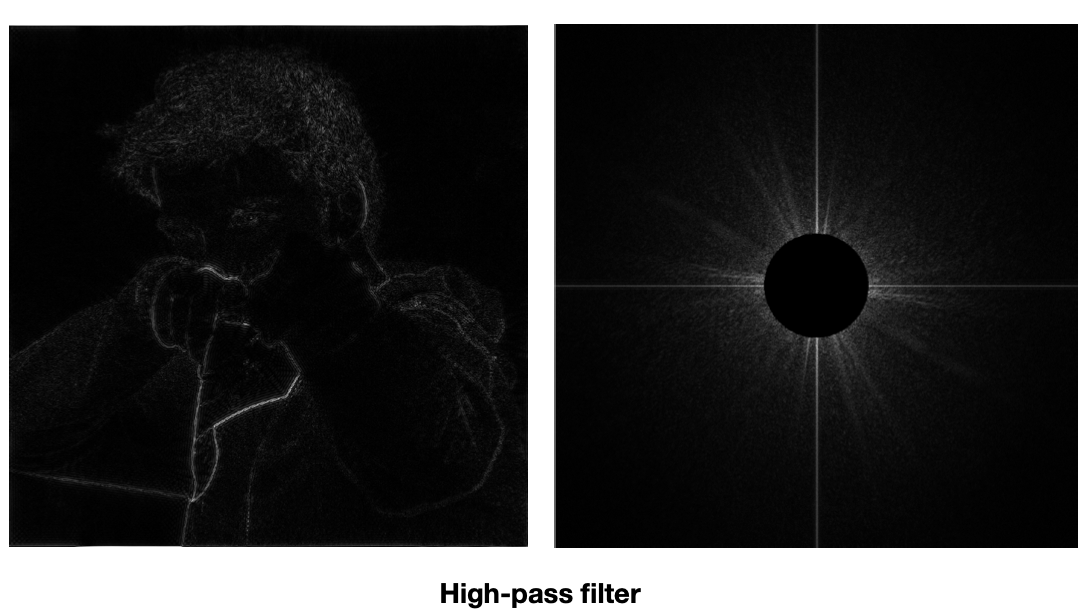
3.1 高通滤波
高通滤波(锐化)是指只有高频可以通过,因此在频域空间内完全抹掉低频信号,将结果还原成图像,形成左图。高频的东西在图像上表示的就是图像的边界。当某一图像的周围突然发生发生了变化,我们就认为他是边界。
3.2 低通滤波
低通滤波(模糊)是指只有低频可以通过,就是把边界给去掉

4 卷积
时域卷积定理:两个时间信号卷积的频谱等于它们频谱的乘积
频域卷积定理:两个时间信号乘积的频谱等于它们的频谱的卷积乘以
对图像进行模糊有两种方法
方法一:拿到一幅图直接用一个卷积滤波器进行卷积操作
方法二:
先傅里叶变换这幅图,将这幅图变到频谱图
将卷积滤波器变到频域上
将两者相乘,乘完后得到的频域的结果,将其逆傅里叶变换,变到时域上
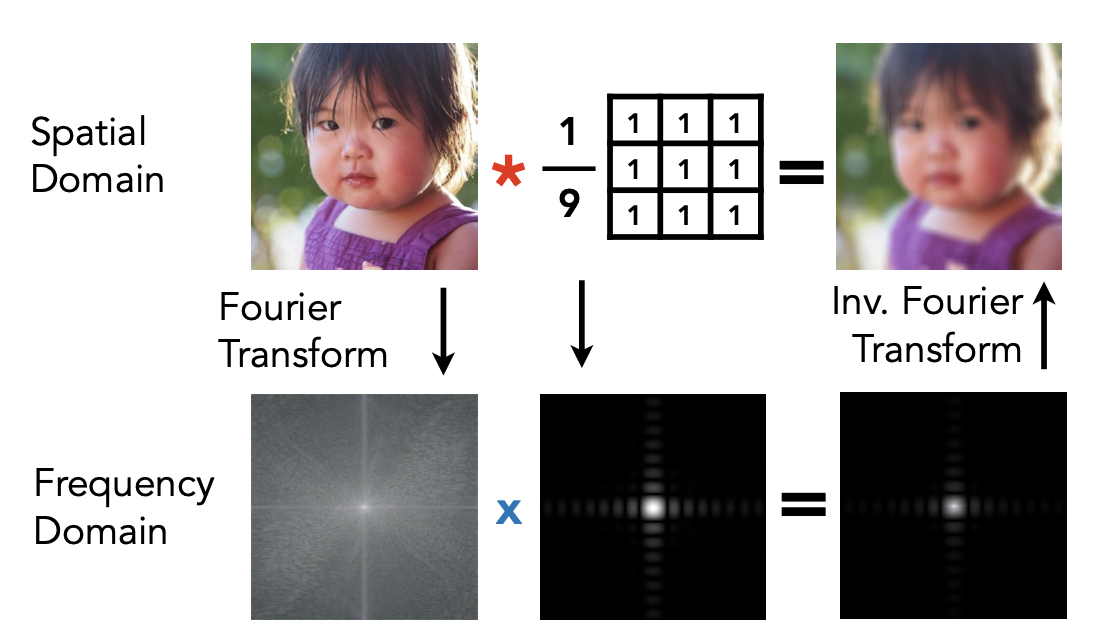
滤波器(滤波器其实就是卷积核的集合,如果只有一个通道,那么滤波器就是卷积核)要乘 是为了不让图像的颜色发生变化,不然每个像素就会是原来这个像素周围九个像素的和,图像就会越滤波越明亮了。
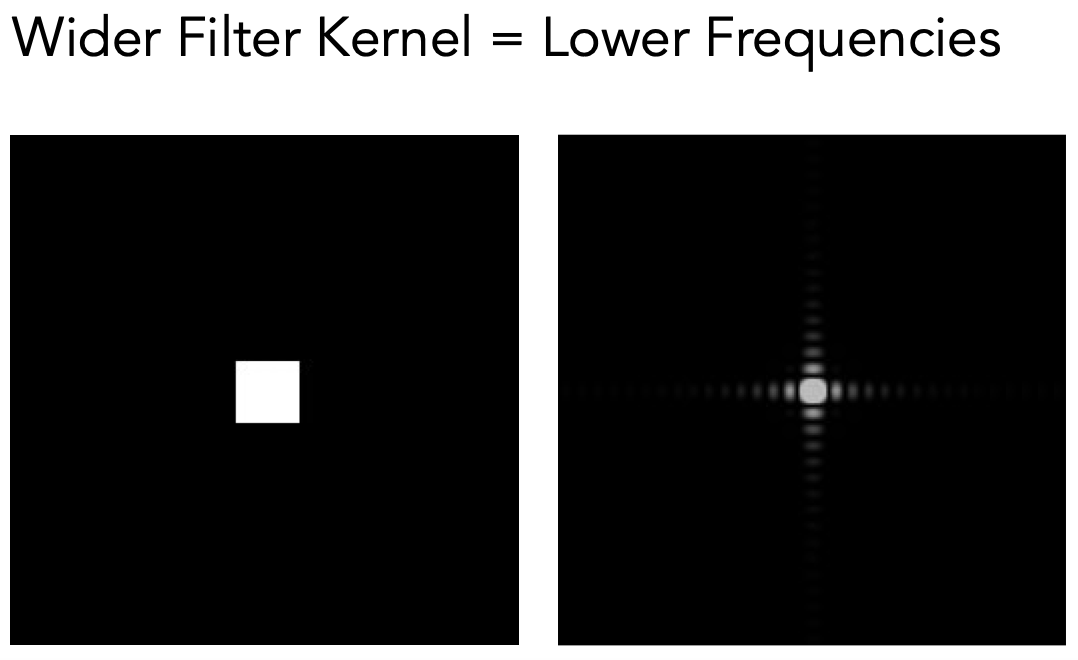
滤波器越大,滤波后的图片就越模糊,留下的频率就越低

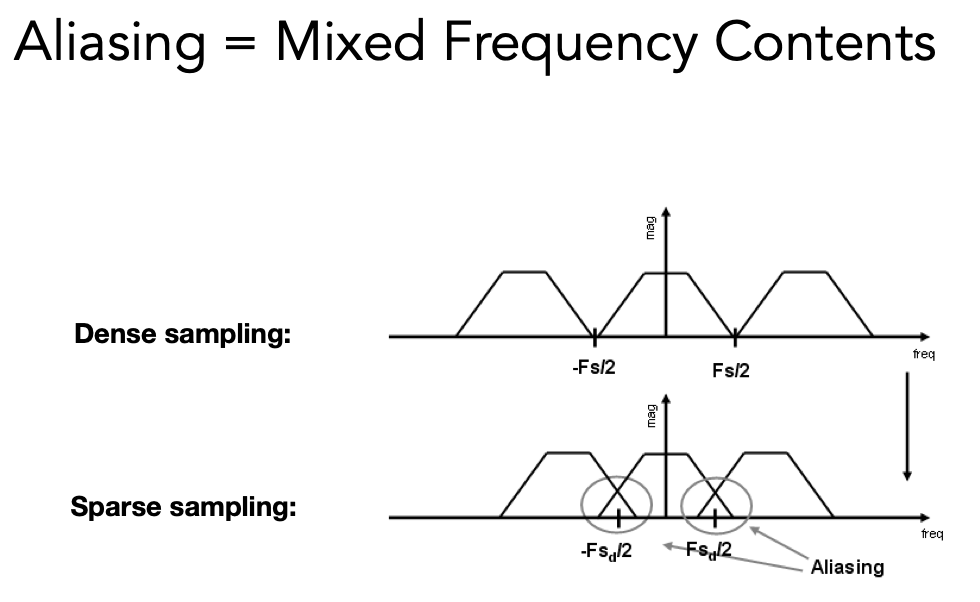
5 走样的原因
采样的间隔不同,会引起频谱不同间隔进行复制,混叠的部分就是走样
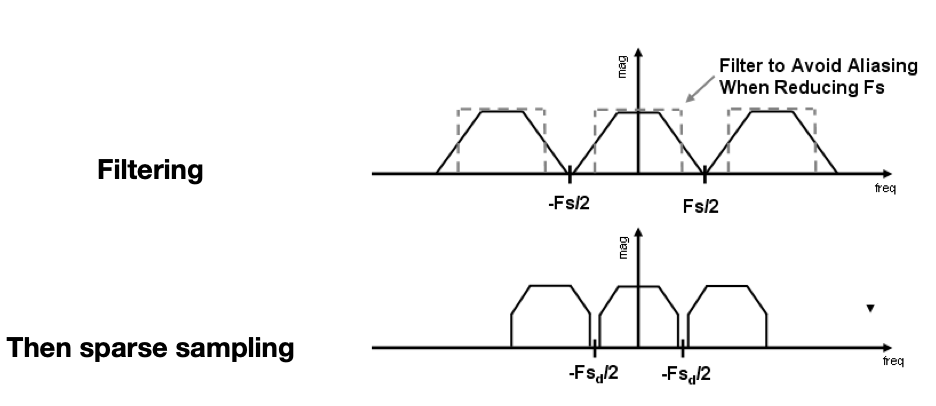
6 反走样
在采样之前先进行低通滤波/模糊(顺序不能反,不能先采样再模糊),上图中混叠的部分(下图中被裁掉的部分)就是高频

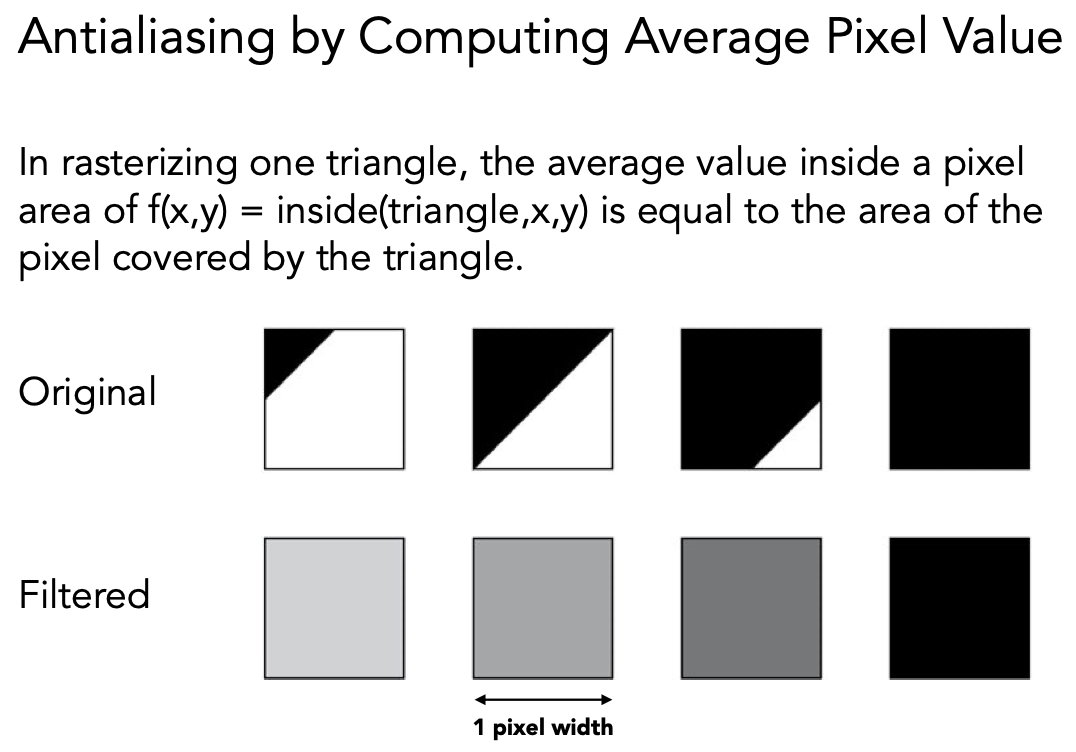
对三角形所覆盖的每个像素都进行卷积(求平均值)
6.1 多重采样抗锯齿 MSAA(Multisample Anti-Aliasing)
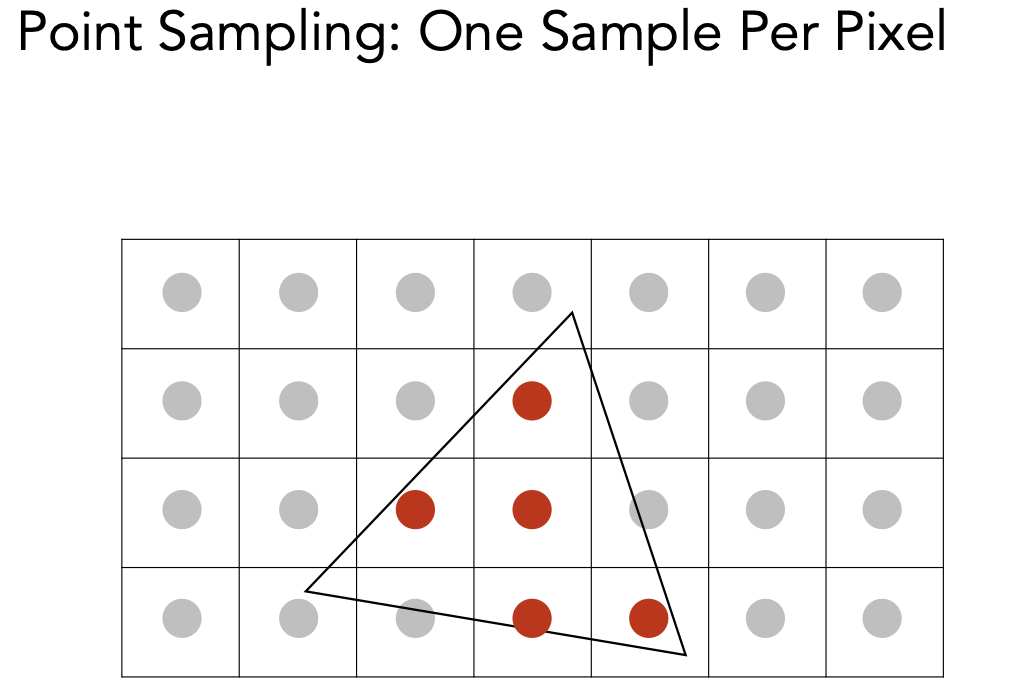
通过更多的样本来近似三角形的覆盖率,并不是提高采样频率,而是把一个像素划分为几个小点,判断这些小点是否在三角形内,再把结果平均起来,就知道三角形覆盖了这个像素的百分之多少 。
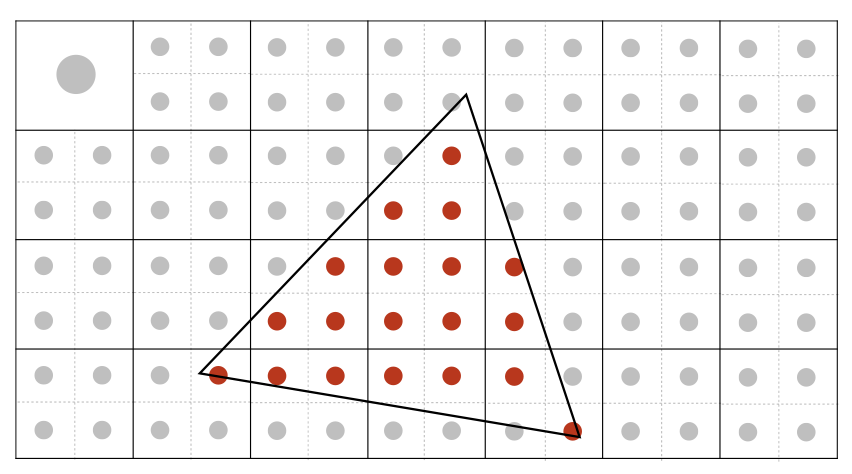
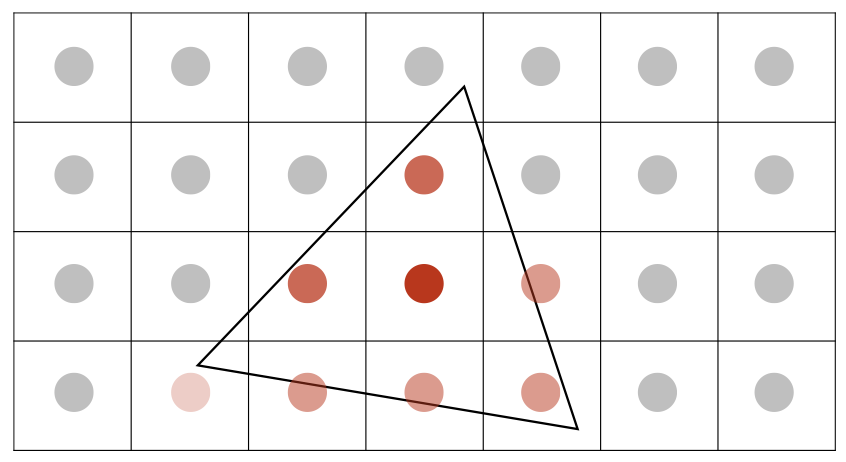
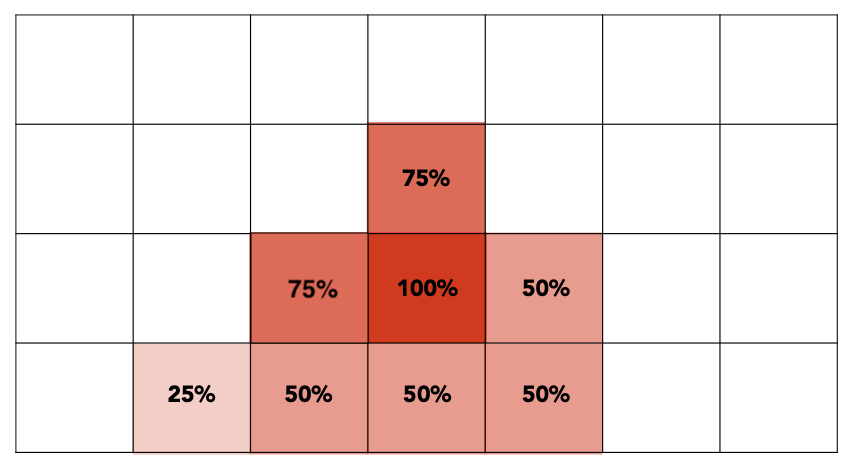
MSAA并没有提高采样频率,而只是对图像进行模糊操作。
其他抗锯齿方案:
- 快速近似抗锯齿 FXAA(Fast Approximate Anti-Aliasing)
- TAA(Temporal Anti-Aliasing)
7 深度测试
使用深度缓存(Z-buffering)算法来进行深度测试。对于每次渲染,Z-buffering 都会同步生成两张图,一个是将所有像素的颜色存在 frame buffer 中,另一个是将所有像素的深度值(每个像素只存最小的深度值)存在 depth buffer 中,对于深度来说,假设深度永远是正的且越小越近,越大越远。

具体算法如下(R 表示 ):


