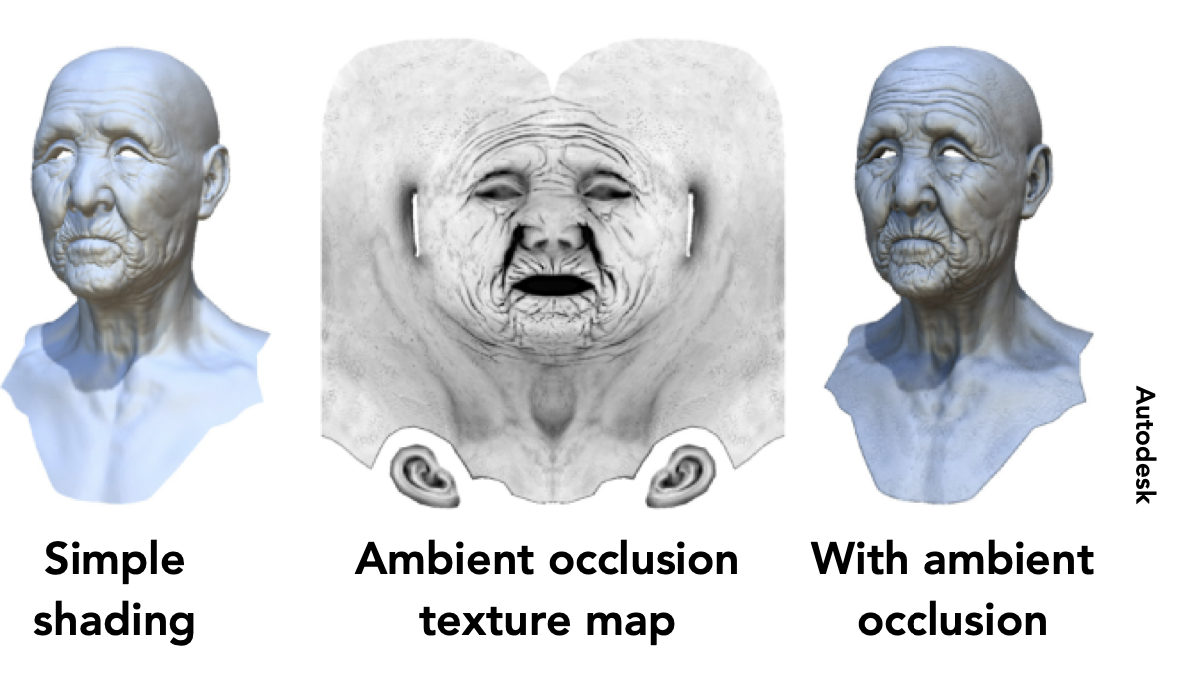
着色(插值、高级纹理映射)
着色(插值、高级纹理映射)
1 重心坐标
重心坐标是为了做三角形内的插值
三角形 ABC(无论是几维)平面内任意一点都可以写成是三个顶点坐标的线性组合,即点 (x, y) 可以用 表示, 就是重心坐标,,且当点在三角形内部时,三个值都是非负的。

重心坐标的几何定义是通过面积比来计算,易得其重心是
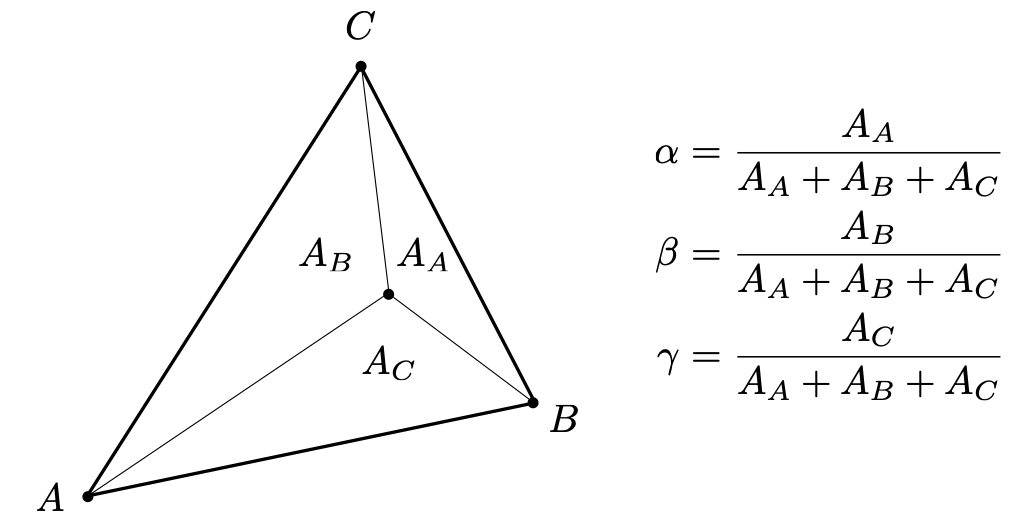
下图是重心坐标的一般公式

1.1 插值
- 插值的作用:确定三角形顶点的值,使三角形内部进行平滑过度(数学定义:插值是一种通过已知的、离散的数据点,在范围内推求新数据点的过程或方法。)
- 插值的内容:纹理坐标、颜色、法线...
- 插值的方法:利用重心坐标进行插值

重心坐标不能保证投影后不变,因此三维空间内的属性应该在三维空间内求插值,而不能投影后再做插值,解决办法就是用逆变换或者透视矫正插值。
2 纹理映射
可以根据每个像素的重心坐标来计算其纹理坐标,通过纹理坐标获得 texcolor,并将 texcolor 赋值给漫反射系数

2.1 纹理过小
双线性插值(Bilinear)是为了解决纹理过小所导致的问题,当纹理过小时,多个 pixel 会映射到同一个 texel 中,那么得到纹理坐标就不是整数,如果采用简单的四舍五入,那么附近几个 pixel 都会是相同的 texel,最后的图片会有明显的锯齿。
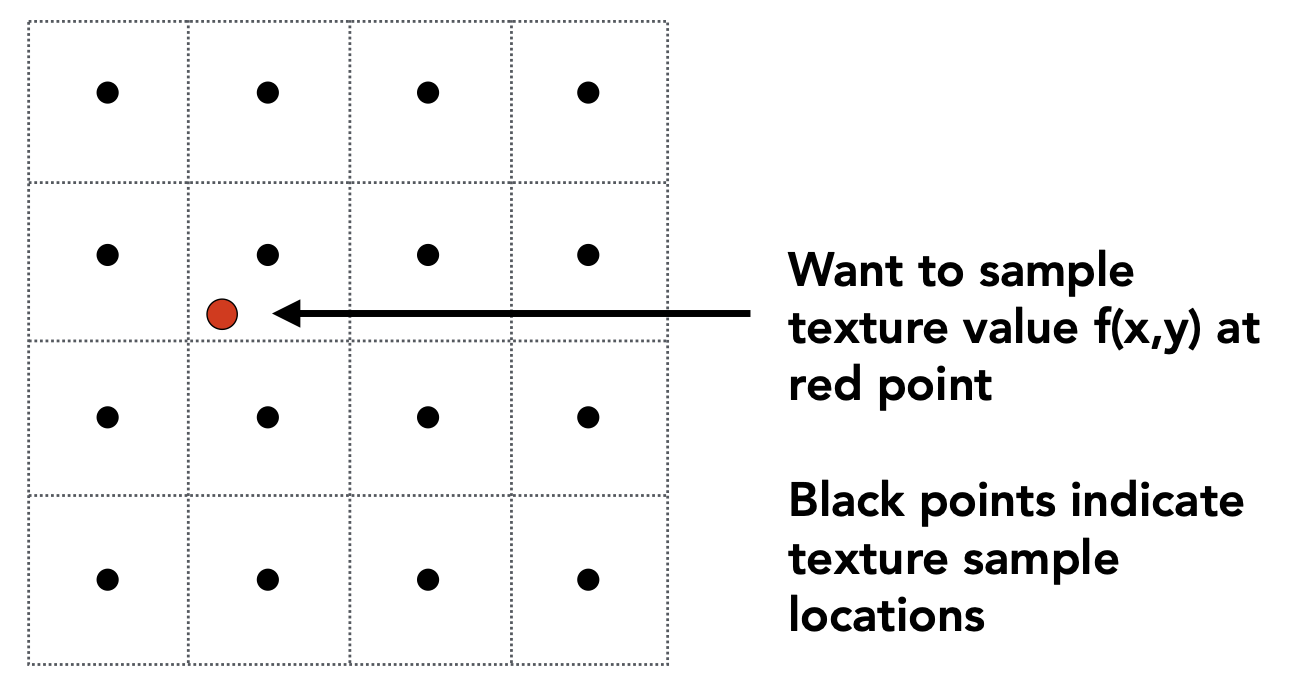
通过最近的 4 个 texel,利用双线性插值可以求得该 pixel 对应的插值。具体做法:
令 ,可以利用线性插值分别求出 I 和 J 的插值
然后再利用 I 和 J 的插值求出 Q 的插值
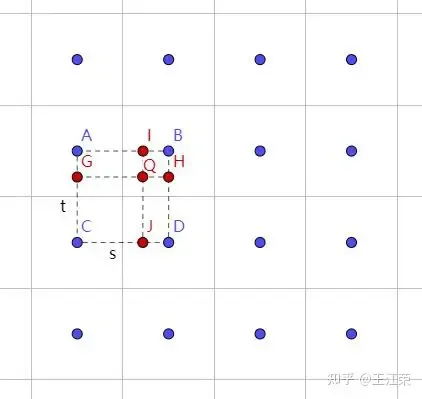
还有一种 Bicubic 的插值算法,通过一个点附近的 16 个 texel,每 4 个一组利用双线性插值求出 4 个插值,再对这 4 个插值再用一次双线性插值求出最后的结果,这个算法效果更好,但是开销很大。
三种算法的效果对比如下

2.2 纹理过大
当纹理过大时,一个 pixel 可能映射到多个 texel,导致采样频率不足,出现摩尔纹
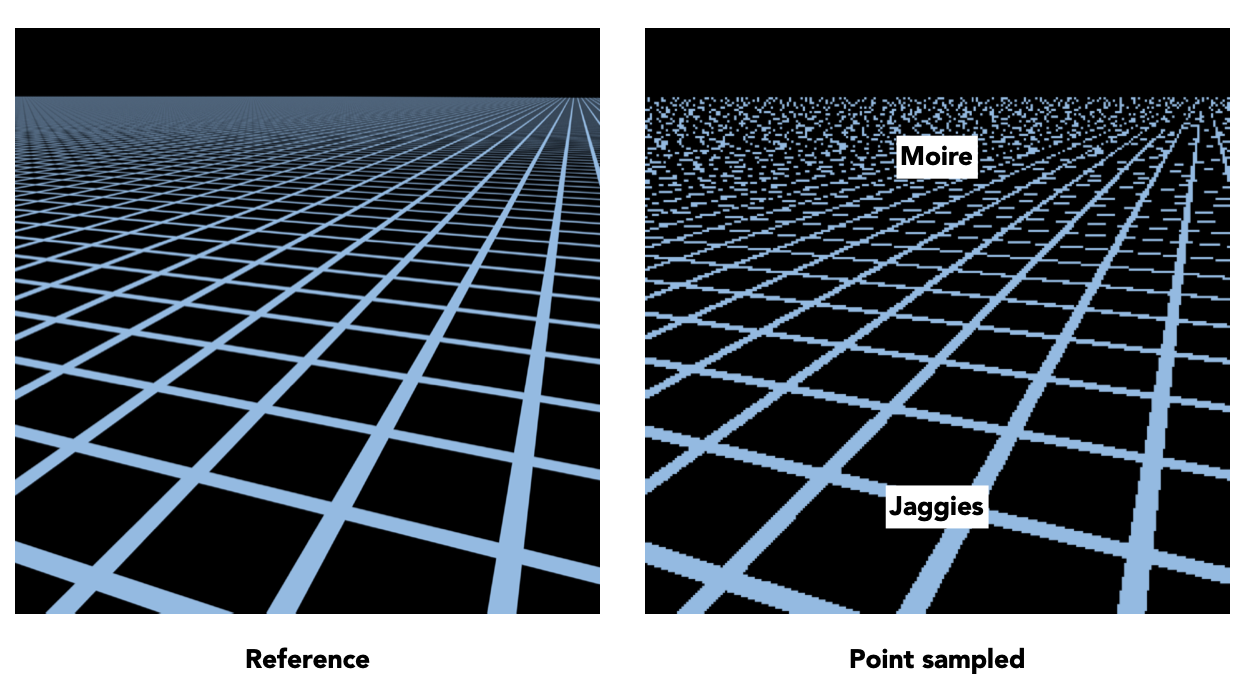
当离 camera 越远时,一个 pixel 会覆盖越多个 texel(不同的像素会有不同的 footprint),也就越来越欠采样。如果只是简单的对多个覆盖的 texel 取均值,那么相邻像素点之间的差距会很大,就会产生摩尔纹。
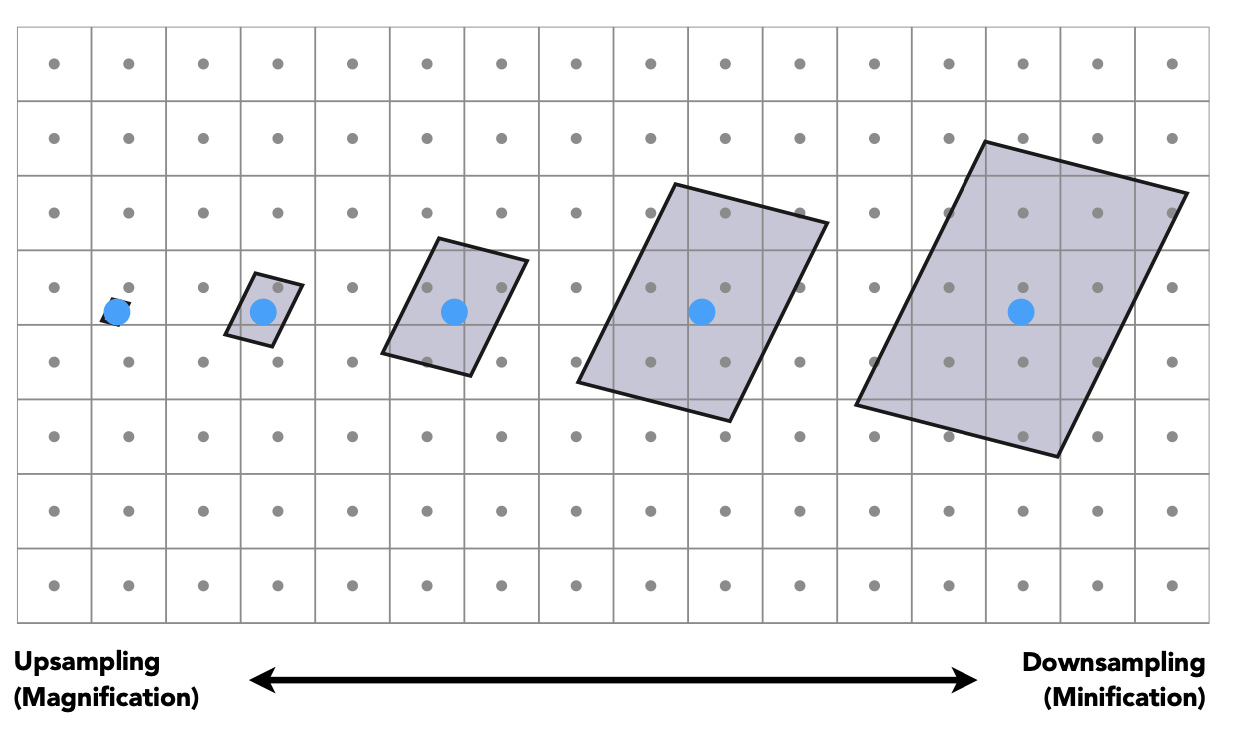
超采样可以解决这个问题,但是开销巨大。超采样类似于光栅化(抗锯齿与深度测试)中的第 6.1 节多重采样抗锯齿 MSAA(Multisample Anti-Aliasing),将一个像素分成更多的采样点。

2.2.1 Mipmap
Mipmap 利用范围查询的方法,速度快,但并不是特别的准确,结果是一个近似值,且只能做正方形的范围查询。其本质就是离线生成多个不同 Level 的纹理,然后通过计算出每个 pixel 所需要使用的 Level,找到对应的 texel。

MipMap 相较于原图只增加了三分之一的存储空间。
计算对应 Mipmap 的 Level D
因为 Mipmap 只能做正方形的范围查询,所以要求出一个 pixel 会覆盖多少个 texel,并将覆盖范围近似成正方形,只需求出正方形的边长 L,其对应的 ,计算所求的 pixel 与周围的几个 pixel 在纹理空间的距离,取其中的最大值就是 L。
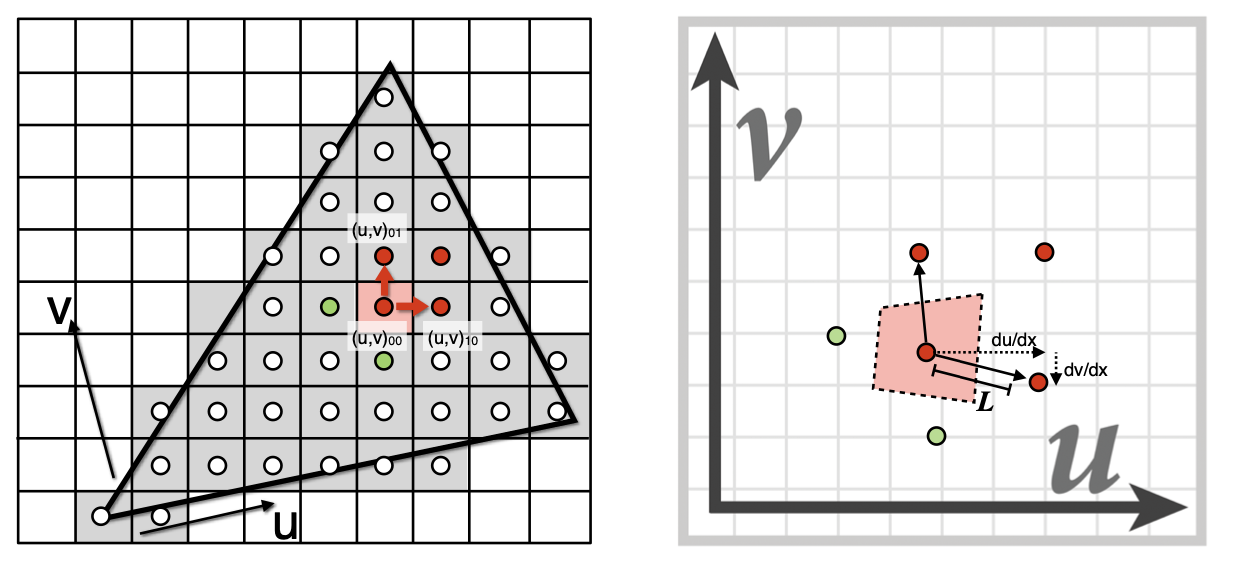
但是 L 并不一定都是 2 的指数倍,所以对应的 D 也不一定是整数,当 D 不是整数时,可以利用三线性插值(Trilinear Interpolation),使最终的结果更加线性

但是 Mipmap 会导致图片远处过于模糊
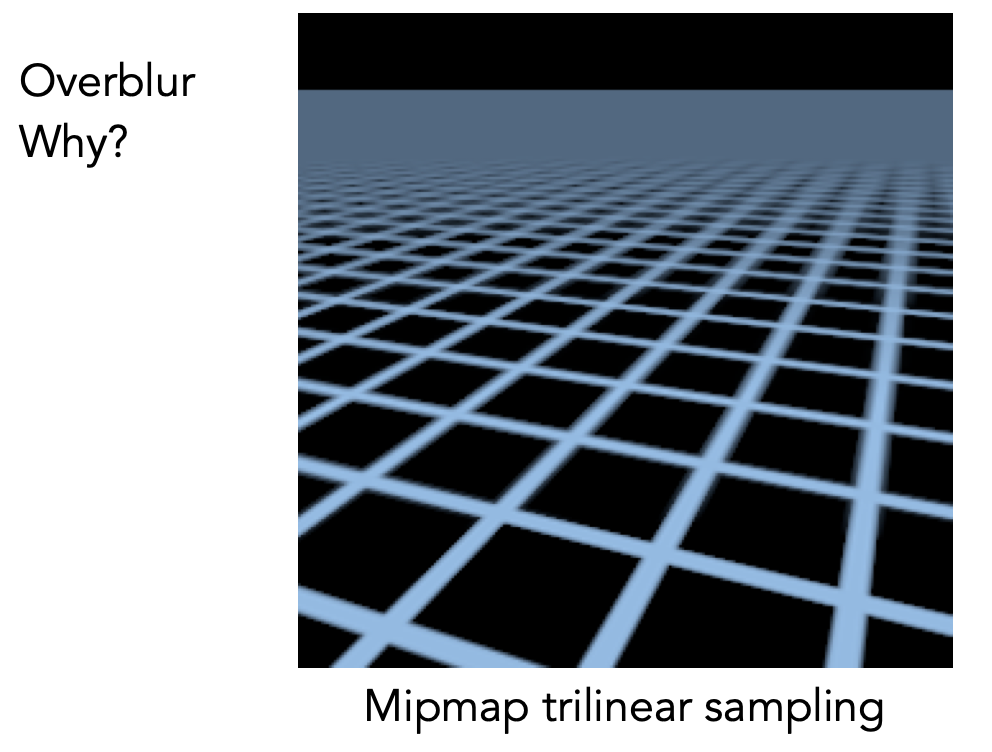
这是因为 Mipmap 只能做正方形的查询,而实际上 pixel 在纹理空间所形成的覆盖区域并不一定是正方形,有可能是长方形甚至不规则图形
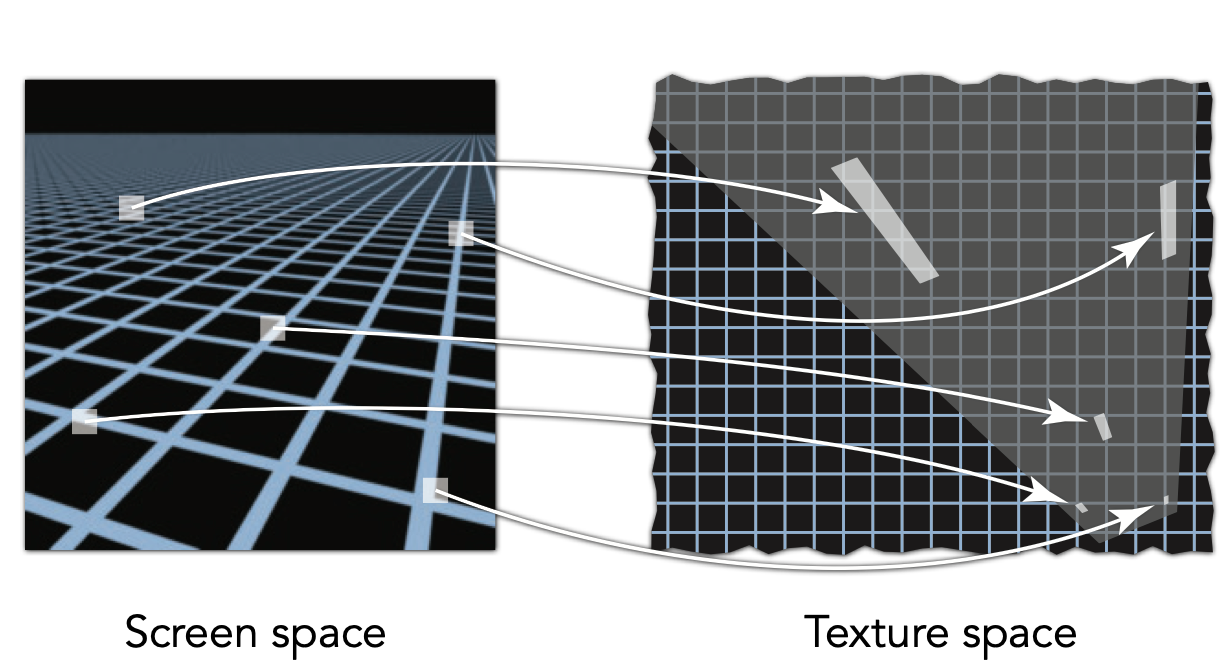
2.2.2 Ripmap / 各向异性过滤(Anisotropic Filtering)
各向异性过滤支持长方形的区域,随着层数的增加,最后的额外存储空间趋向于原图的三倍

对于不规则的图形,各向异性过滤也无法解决,可以使用 EWA 过滤

3 纹理应用
在现代 GPU 中,纹理 = 内存 + 范围查询(滤波)
3.1 环境光映射(Environment Map)
因为几乎只有观察方向对环境光起到影响,所以各个方向的光源可以用一个球体进行存储。

类比地球仪,把它展开,就可以把球面信息转换到平面上,从而得到环境 texture。

类比地球仪,在极点存在拉伸和扭曲问题,解决方法就是 Cube Map,在原来球体上取一个包围盒,一个立方体,把环境光的信息存放在立方体上。
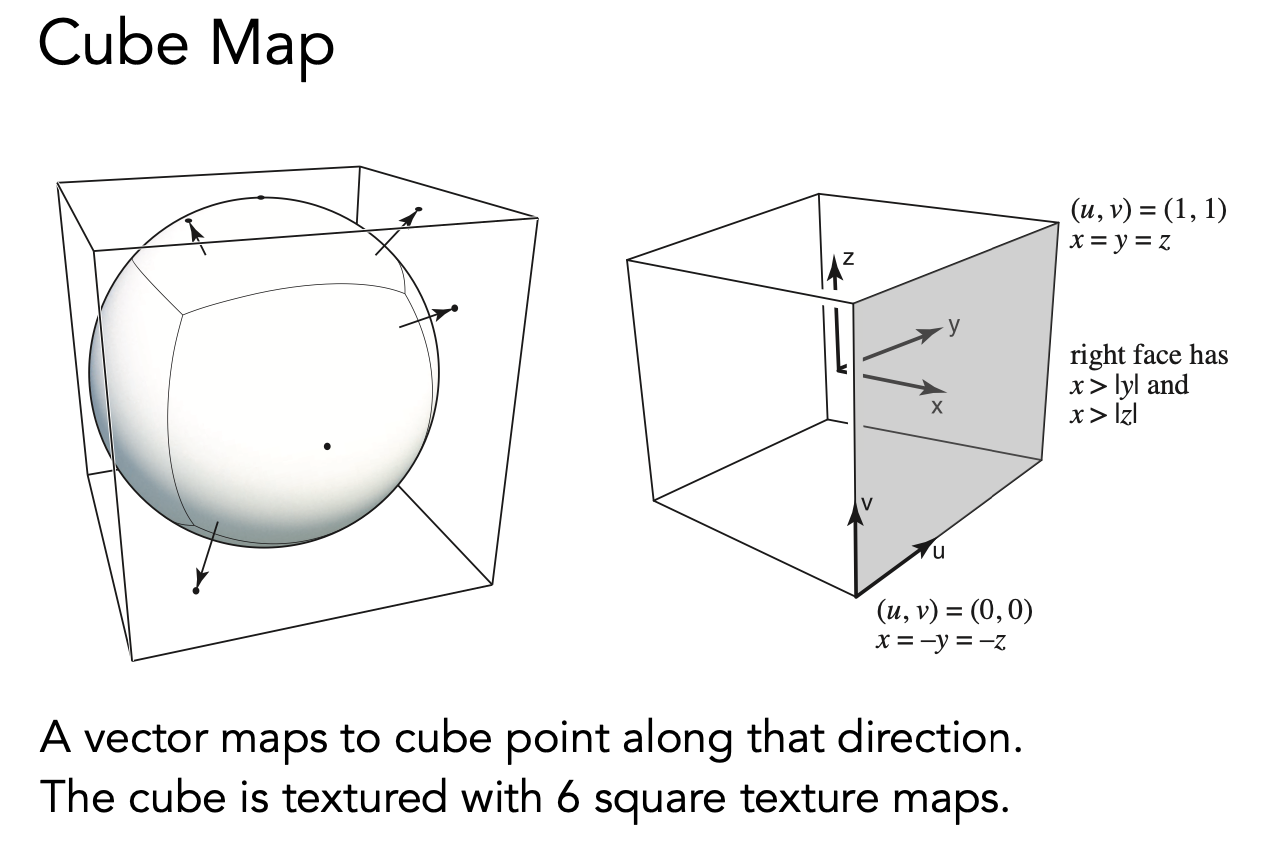

与球形环境光贴图相比,解决了两极的扭曲问题,计算时需要先找到对应的面在去查询而不是直接根据角度在球面上读取,但是这个计算过程非常快,几乎没什么影响。
3.2 凹凸 / 法线贴图(Bump / Normal Mapping)
纹理处理可以描述颜色之外,还可以定义不同位置的任何属性,可以定义一点的相对高度,这个相对高度指的是先定义一个基础表面,在这个基础表面上沿着法线向上向下变化的偏移量。这样不改变几何,只改变法线,着色后会产生明暗对比,人们的视觉就会认为物体表面有凹凸。

给一个像素的法线做个扰动,可以通过高度的变化来求出改变后的法线,下图中黑色的线是原来光滑的平面,黄色的线是扰动后的面,可以通过微分的方法来求改变后的法线。

将问题简单为 2D,假设原本表面是一维函数,P 点的法线是 (0, 1),只要通过微分求出 P 点点切线,切线与法线是垂直的,即点积为 0,最后做个归一化就能得到法线。
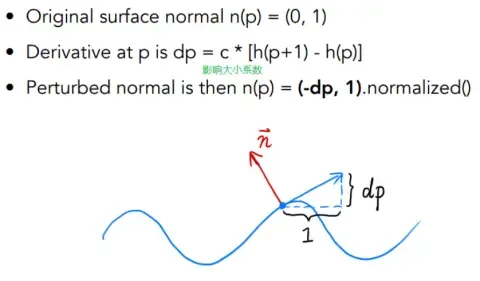
实际使用是 3D 的,思路类似

3.3 位移贴图(Displacement Mapping)
位移贴图和凹凸贴图使用的是一样的纹理,输入是一样的,但位移贴图会真的把三角形的顶点做一个位置移动。呈现的效果也是不一样的,如下图左侧凹凸贴图在渲染过程中改变法线,欺骗人们的眼睛,仔细观察会发现表面虽然看起来凹凸不平,凸起的部分也没有阴影,而位移贴图是实际改变了几何体的顶点,凸起部分会有阴影,效果也更加真实。

3.4 三维纹理
三维纹理,定义空间中任意一点的纹理。并没有真正生成纹理的图,而是定义一个三维空间的噪声函数经过各种处理,变成需要的样子。
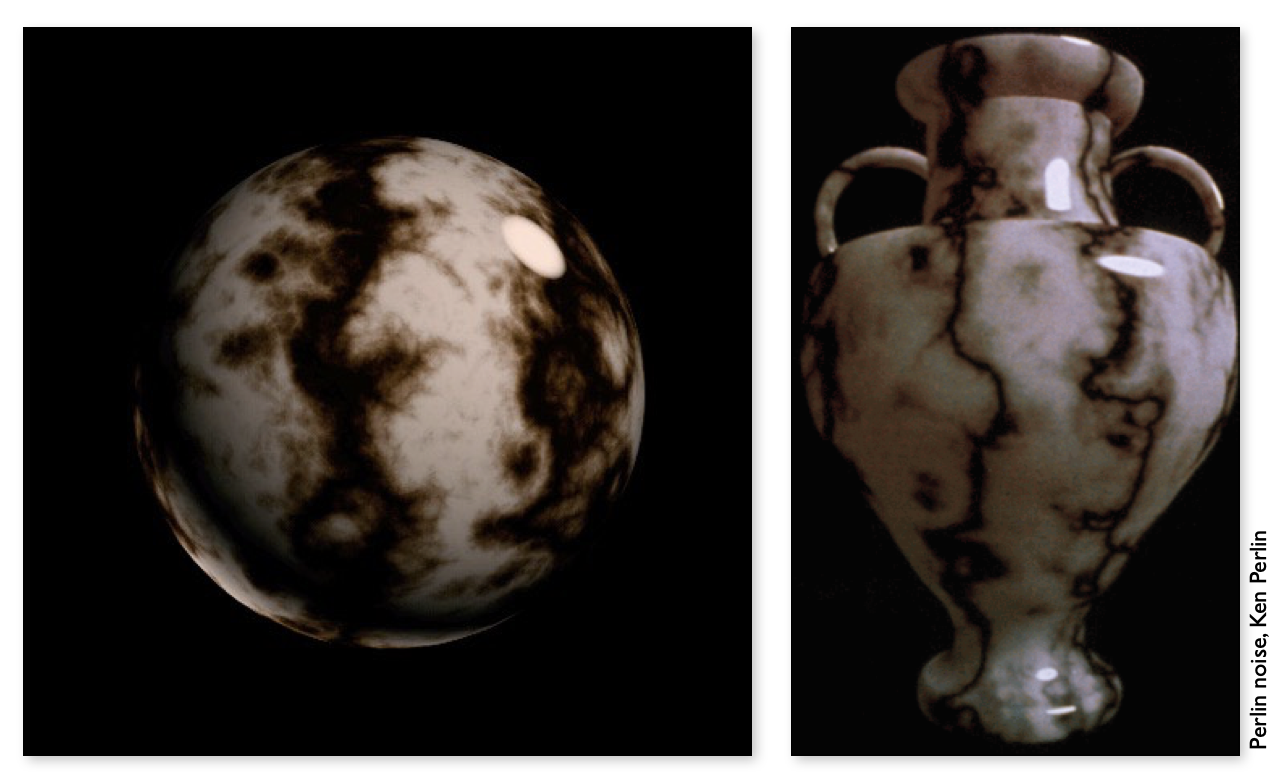
3.5 阴影纹理
阴影是提前计算好的,直接写在 texture 中