变换(二维与三维)
...约 693 字大约 2 分钟
变换(二维与三维)
1 线性变换
注意:线性变换的矩阵是与向量同维度的,如果不同维度的则是齐次坐标(3.2的内容)

1.1 缩放变换

1.2 镜像变换
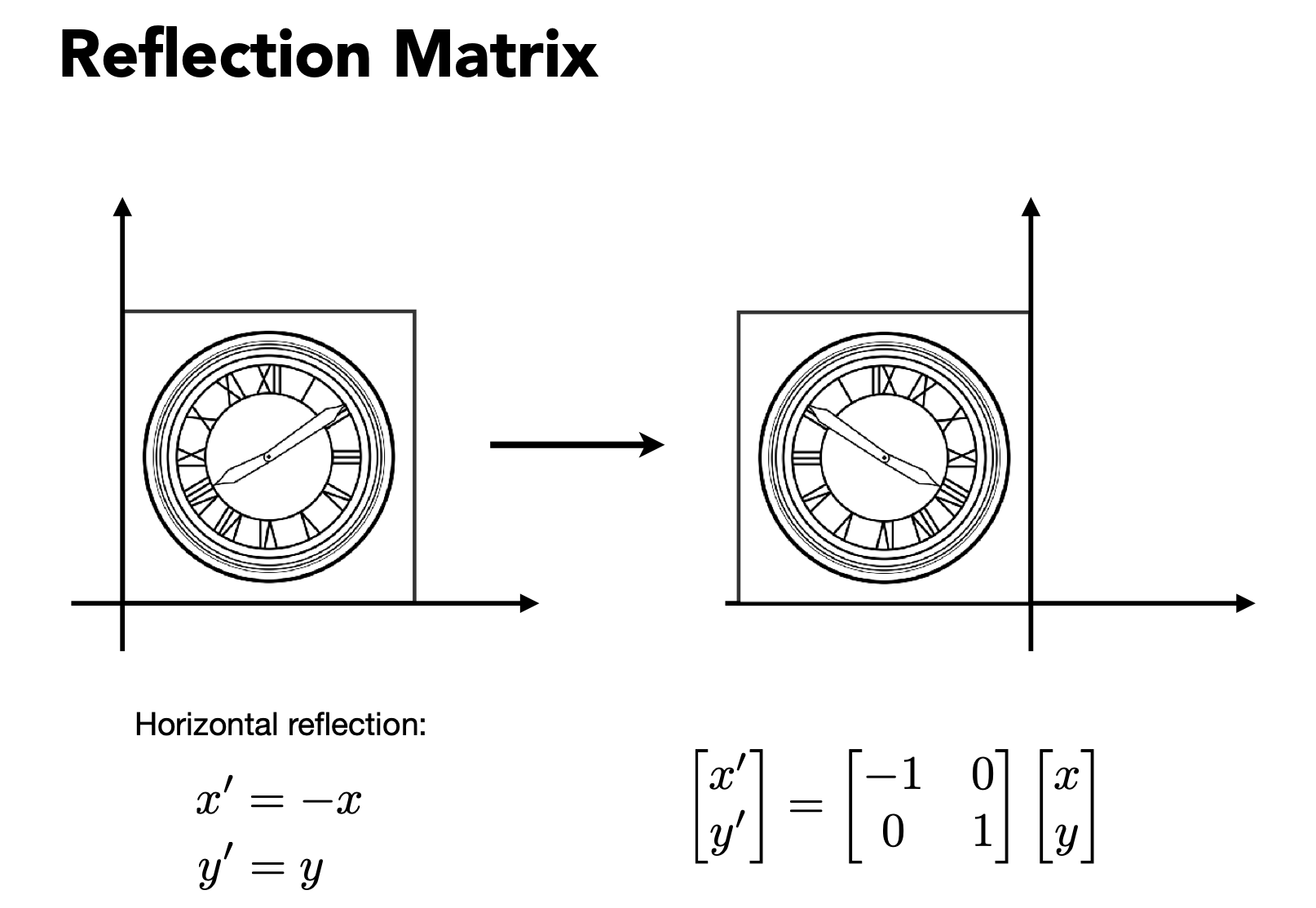
1.3 剪切变换

1.4 旋转变换
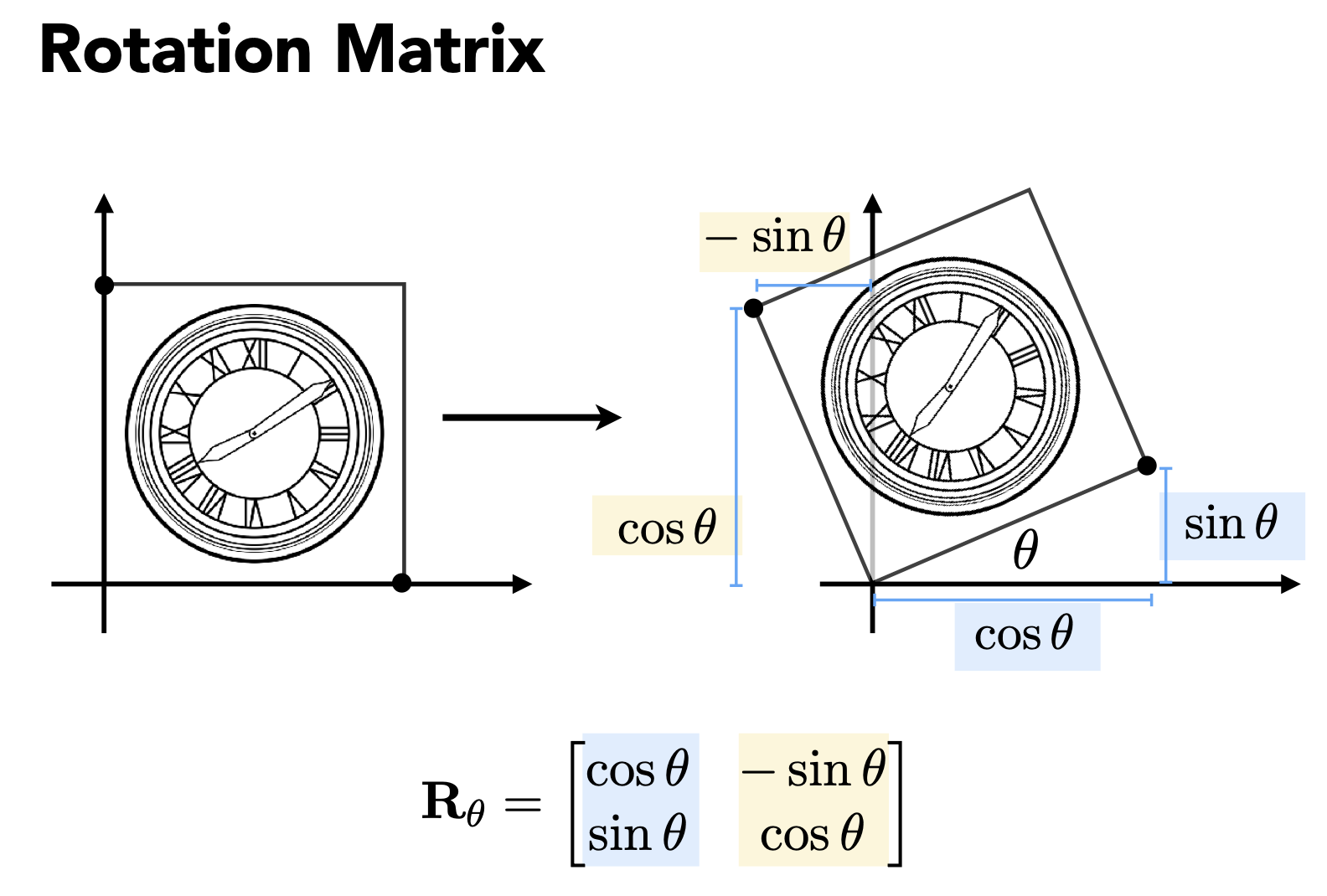
推导过程:

2 齐次坐标
引入齐次坐标的原因:无法用与向量同维度的矩阵来表示平移变换

增加一个维度来表示齐次坐标,其中二维中的点的第三维为 1,二维向量的第三维为 0

只要第三维非0表示的就是点,两个点相加表示的是两个点所连成的线的中点

仿射变换=线性变换+平移变换,可以用齐次坐标来表示仿射变换

因此线性变换也可以用齐次坐标来表示

齐次坐标的代价(trade off):多一个维度
3 逆变换
- 一个图形 A 通过变换矩阵 M 得到图形 B,图形 B 可以通过 M 的逆矩阵 得到原来的图形 A(这个过程称为逆变换)
- 旋转变换矩阵 M 是正交矩阵,即
4 变换的组合
- 一个复杂的变化可以通过许多简单的变换组合得到
- 变换的顺序十分重要(矩阵乘法不满足交换律)
- 矩阵乘法中是从右到左的顺序进行变换, 是对 x 先进行 的变换,再进行 的变换...但是矩阵乘法满足结合率,因此也可以先将矩阵先乘好后再对 x 进行变换
5 三维变换
与二维类似,齐次坐标用 4 维表示即可,其他与二维的类似


先线性变换再平移变换
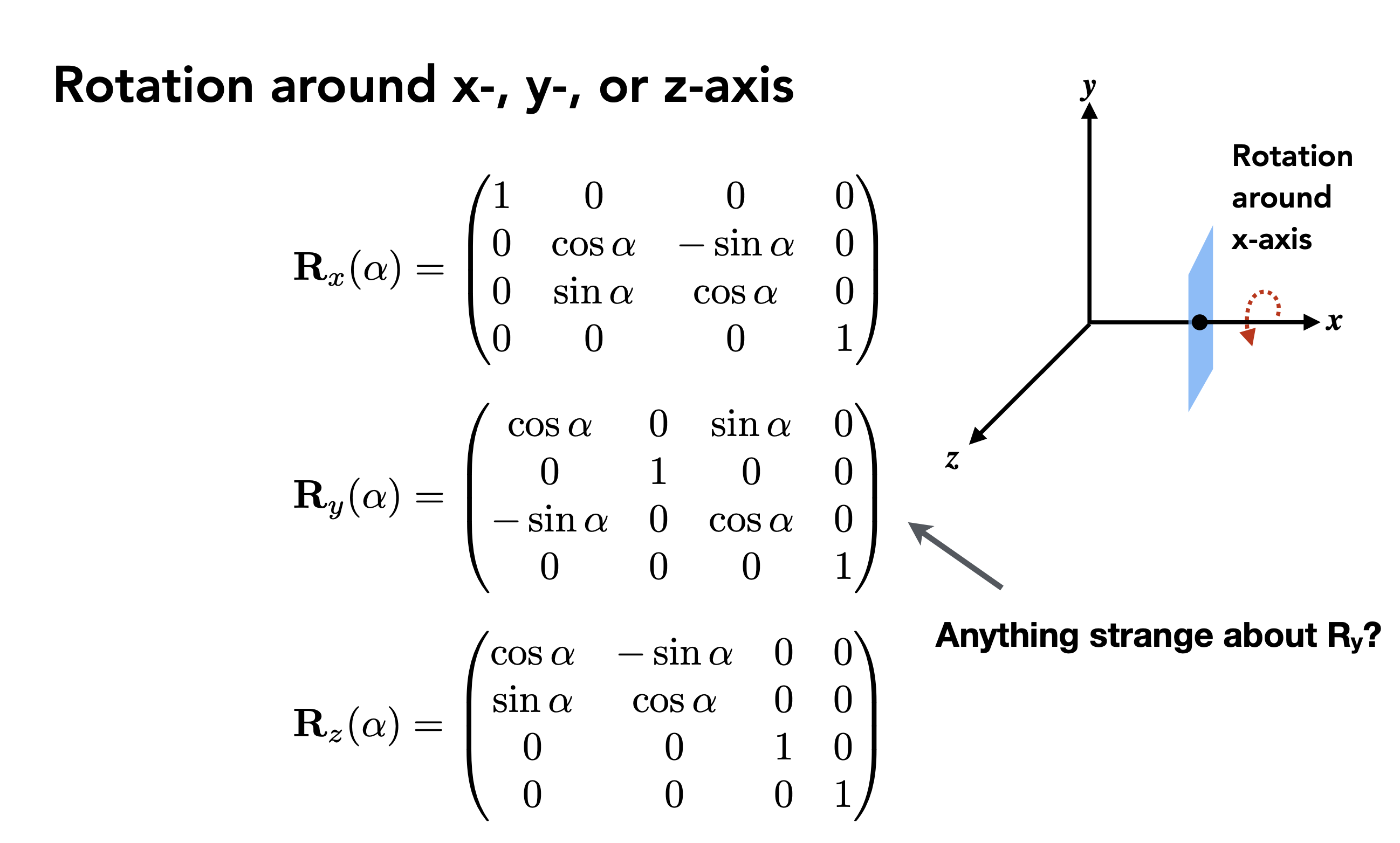



对于以 n 为轴转动 角度可以使用罗德里格斯公式,n 轴是过原点的;要想真的绕任意轴 m 旋转,可以先将图像平移到旋转轴 m 过原点,再利用罗德里格斯公式(I 为单位矩阵),最后对平移进行逆变换。

初始向量 v 绕 n 轴转 角得到, 是对应的旋转矩阵
Powered by Waline v2.15.5
