光栅化(三角形的离散化)
...约 692 字大约 2 分钟
光栅化(三角形的离散化)
将 的标准立方体中的内容经过一系列变换最终转换为像素从而呈现在屏幕上的过程就称为光栅化。
首先需要定义视锥(frustum),包含两个属性:
- 宽高比(aspect ration)
- 可视角度(fov),分为垂直可视角度(fovY)和水平可视角度(fovX),知道宽高比和其中一个可视角度就可以求出另一个可视角度
两根红线之间的夹角就是 fovY

可以通过宽高比和可视角度来求出 l,r,b,t(默认相机已经在原点,因此可观测区域的 l=-r, b=-t)

1 屏幕空间
定义如下:
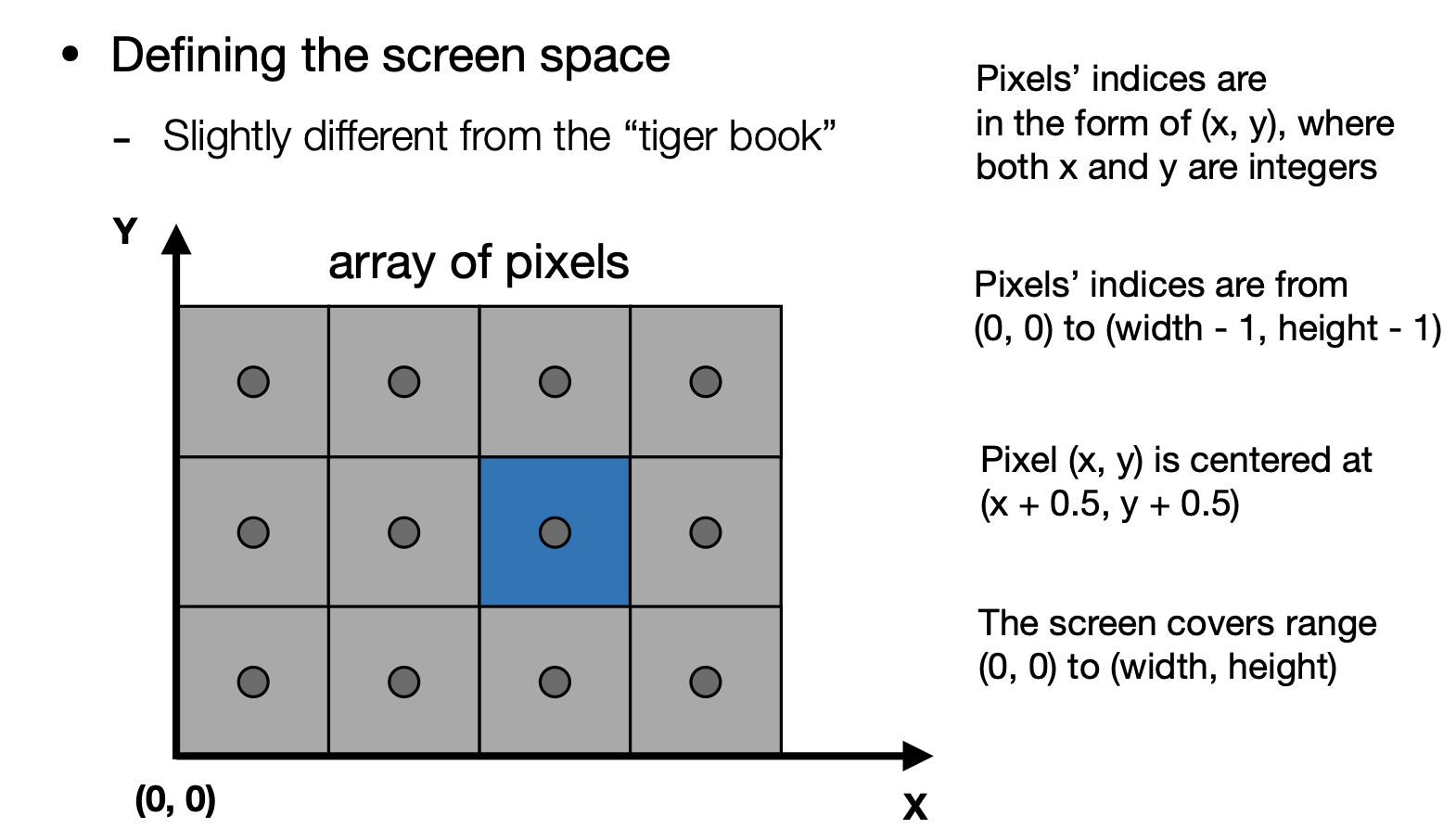
2 视口变换
从 的标准立方体映射到屏幕空间:
- 暂时忽略 z
- 只将 的内容显示到 [0, width] * [0, height] 的屏幕空间内(需要进行缩放,并将 xOy 平面的中心平移到屏幕空间的中心,这个变换就叫视口变换)
视口变换矩阵
3 三角形
光栅化选择三角形的原因:
- 三角形是最基本的多边形,没有比三角形边更少的多边形
- 其他多边形都可以拆分为三角形
- 三角形必定在一个平面内
- 容易定义三角形的里外
- 三角形的三个点定义好后,三角形内任意一点可以通过重心座标插值(barycentric interpolation) 来计算得到
4 判断一个像素的中心点与三角形的位置关系
给定一个三角形,在像素的中心进行采样,来判断中心是否落在三角形内(如何判断是否在三角形内,可以看2.2的内容)

但是遍历所有像素开销太大,如下图中白色那一列的像素根本没有碰到三角形,所以只要遍历蓝色区域就可以了,我们知道三角形三个顶点的坐标,有了 Xmin, Ymin, Xmax, Ymax 就可以得到蓝色的区域,蓝色区域就叫做包围盒 。
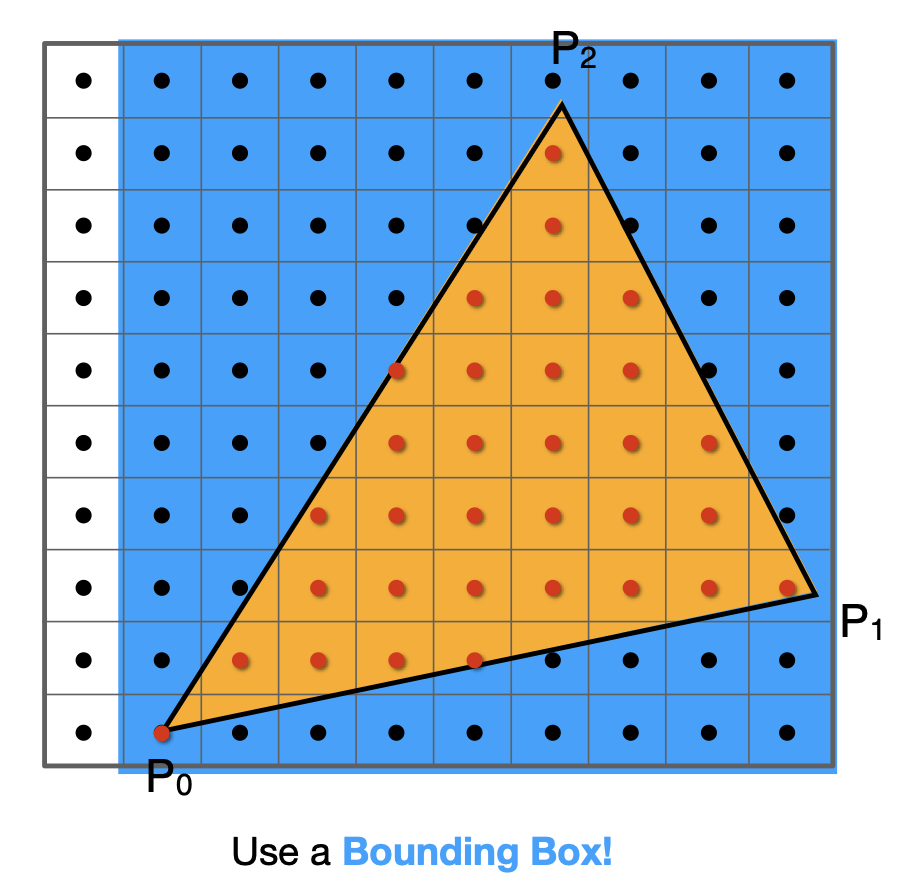
采样完成后,因为每个像素都是最小单位,像素内的颜色必须一样,所以我们会得到这样一副图
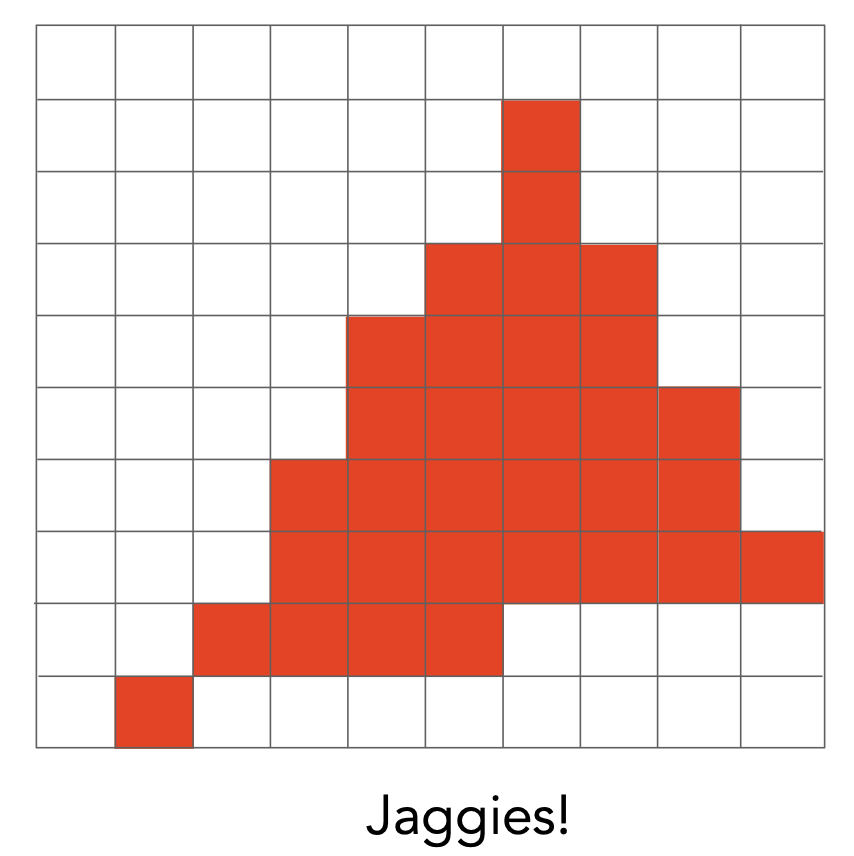
这看起来和初始的三角形差别很大,有明显的锯齿(jaggies),锯齿的学名叫走样(aliasing),之后就会学抗锯齿/反走样
Powered by Waline v2.15.5
