几何(曲线与曲面)
...约 706 字大约 2 分钟
几何(曲线与曲面)
1 贝塞尔曲线
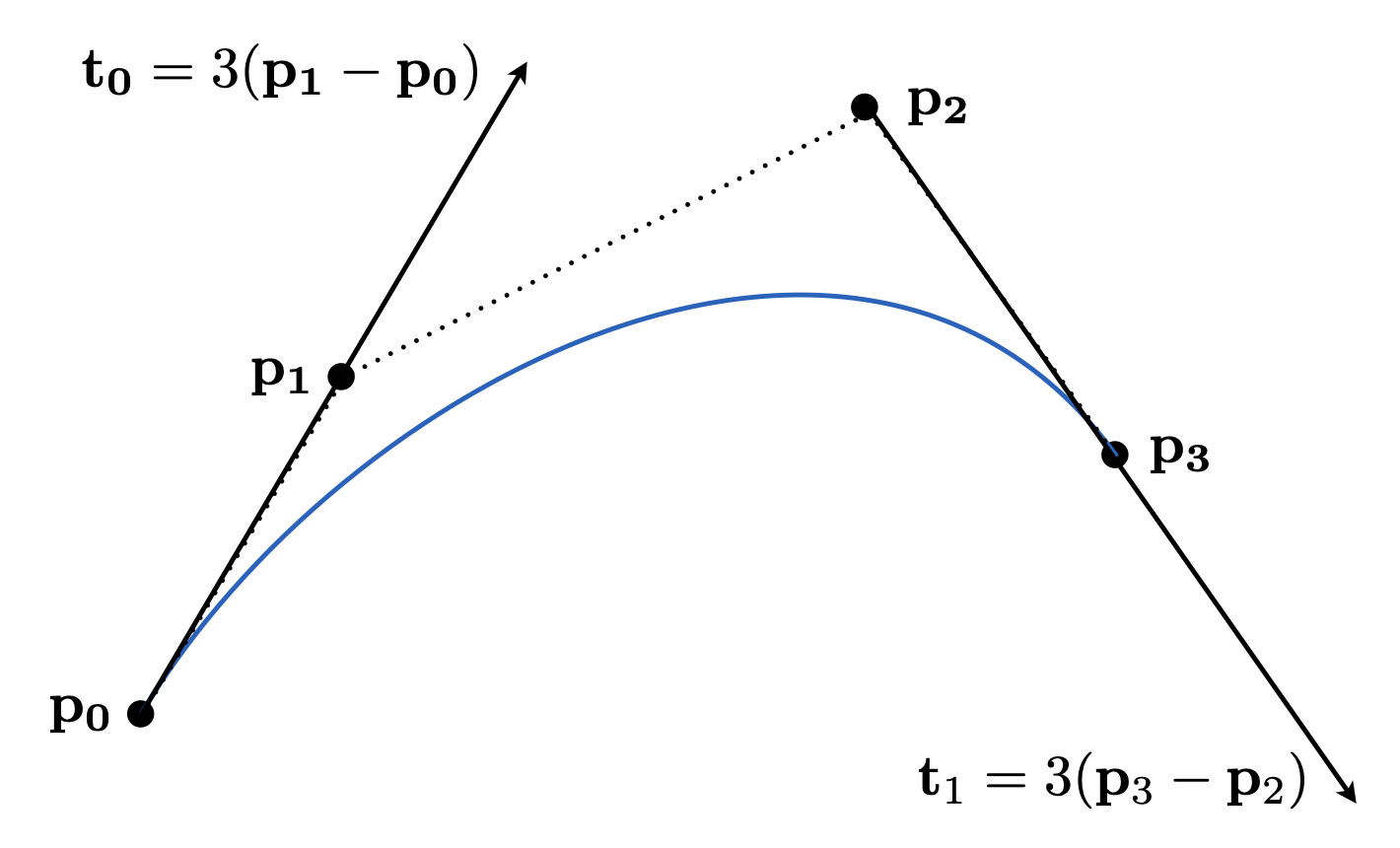
为控制点,蓝色曲线就是贝塞尔曲线,曲线会与初始与终止端点相切,并且经过起点与终点
1.1 de Casteljau Algorithm
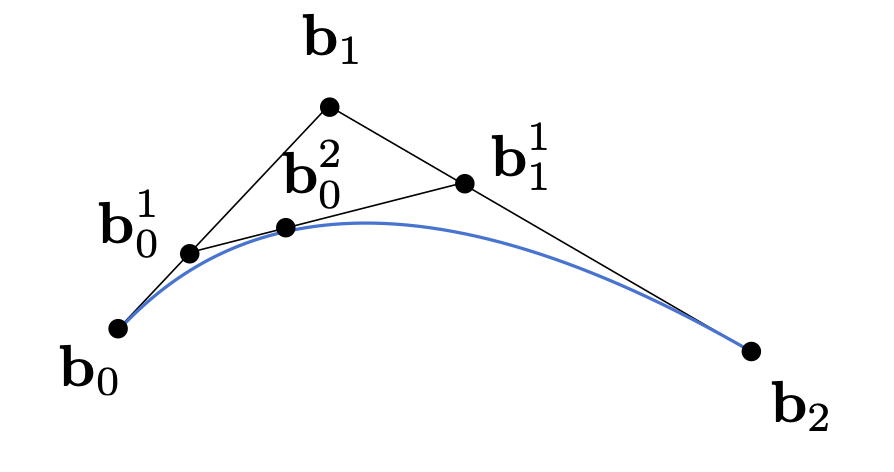
de Casteljau 算法描述了如何用多个点画出一条贝塞尔曲线,其核心是线性插值和递归。第一步选定一个参数 ,在 线段上利用 t 值进行线性插值,即 ,得到 之后在 线段上重复做相同的线性插值得到 ,再在 线段上递归进行相同操作得到 ,对所有的 都重复上述过程后就能得到贝塞尔曲线,这是求二阶贝塞尔曲线的过程。
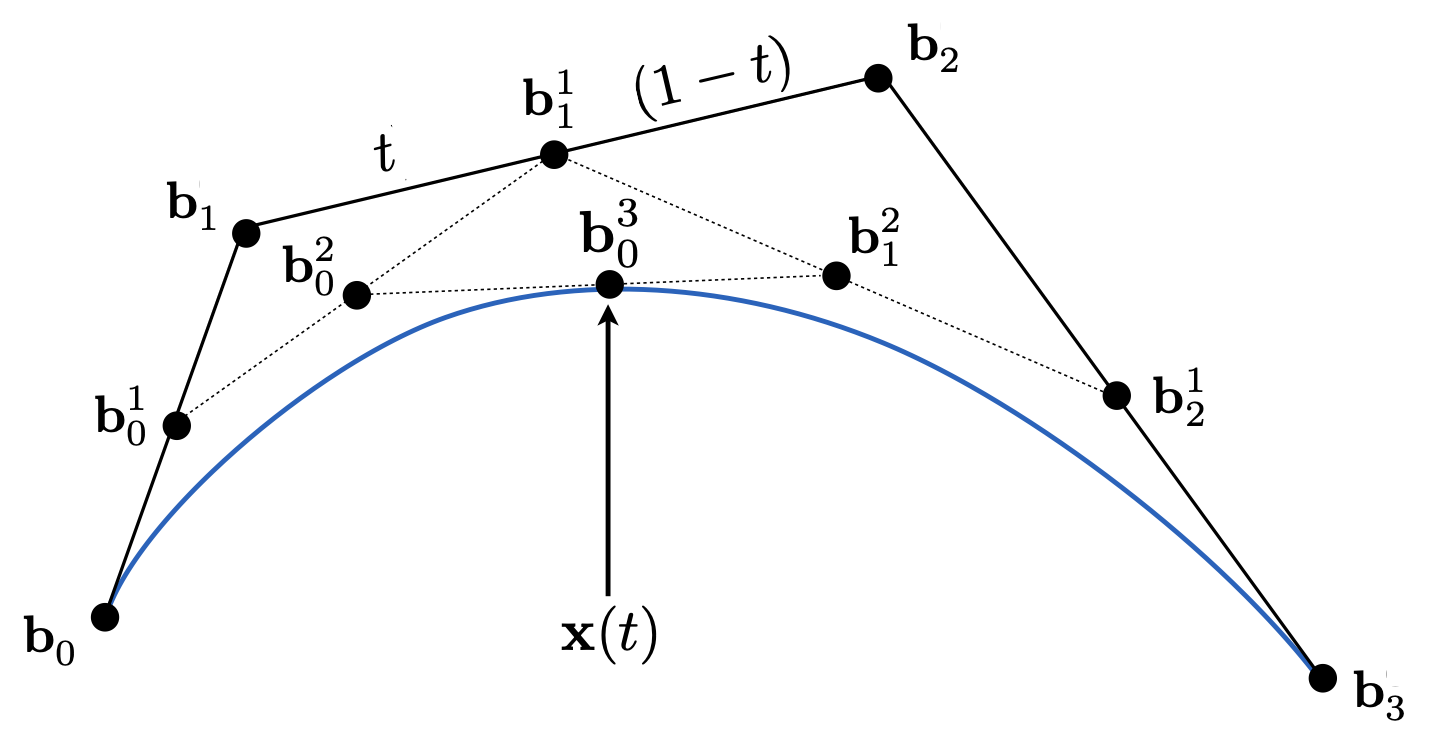
对于三阶贝塞尔曲线过程也类似,只是比二阶多一次递归
1.2 代数式表达
二阶贝塞尔曲线展开:
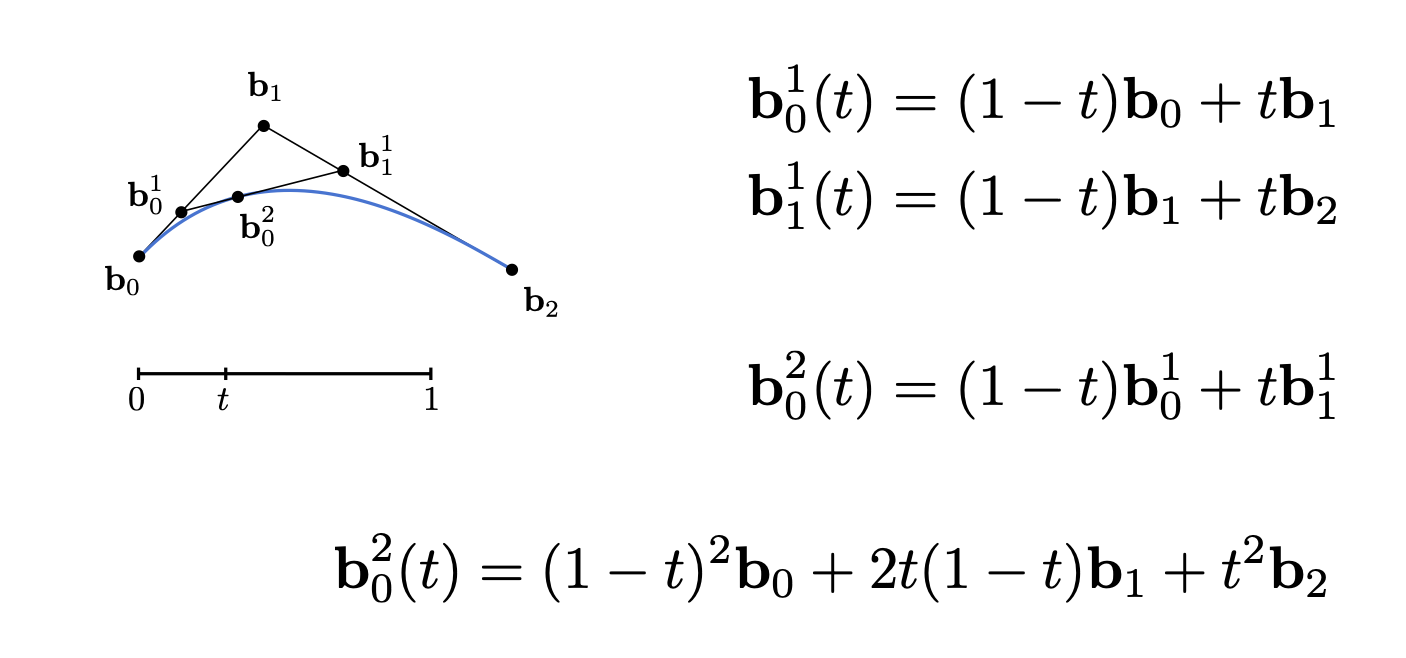
推广到 n 阶贝塞尔曲线的代数表达式:

伯恩斯坦多项式中的
1.3 贝塞尔曲线的性质
- 必定经过起始与终止控制点
- 必定经与起始与终止线段相切
- 具有仿射变换性质,可以通过移动控制点移动整条曲线,但是投影之后会改变
- 凸包性质,曲线一定不会超出所有控制点构成的多边形范围
- 凸包:墙上许多钉子,用一条橡皮筋包住最外边的钉子,再松手,橡皮筋收缩后的外框就是凸包
1.4 分段贝塞尔曲线
将一条高阶曲线分成多条低阶曲线的拼接,通常用3阶曲线来拼接
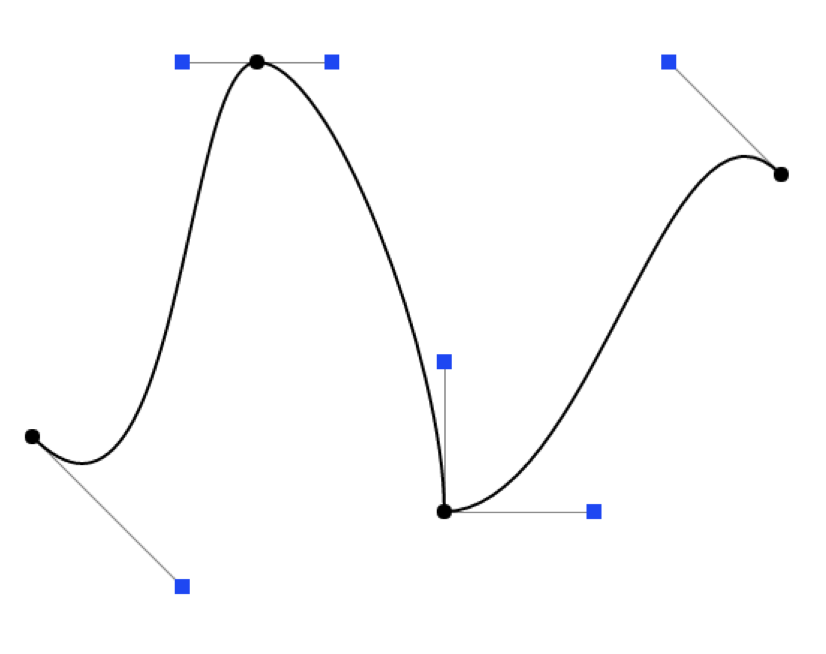
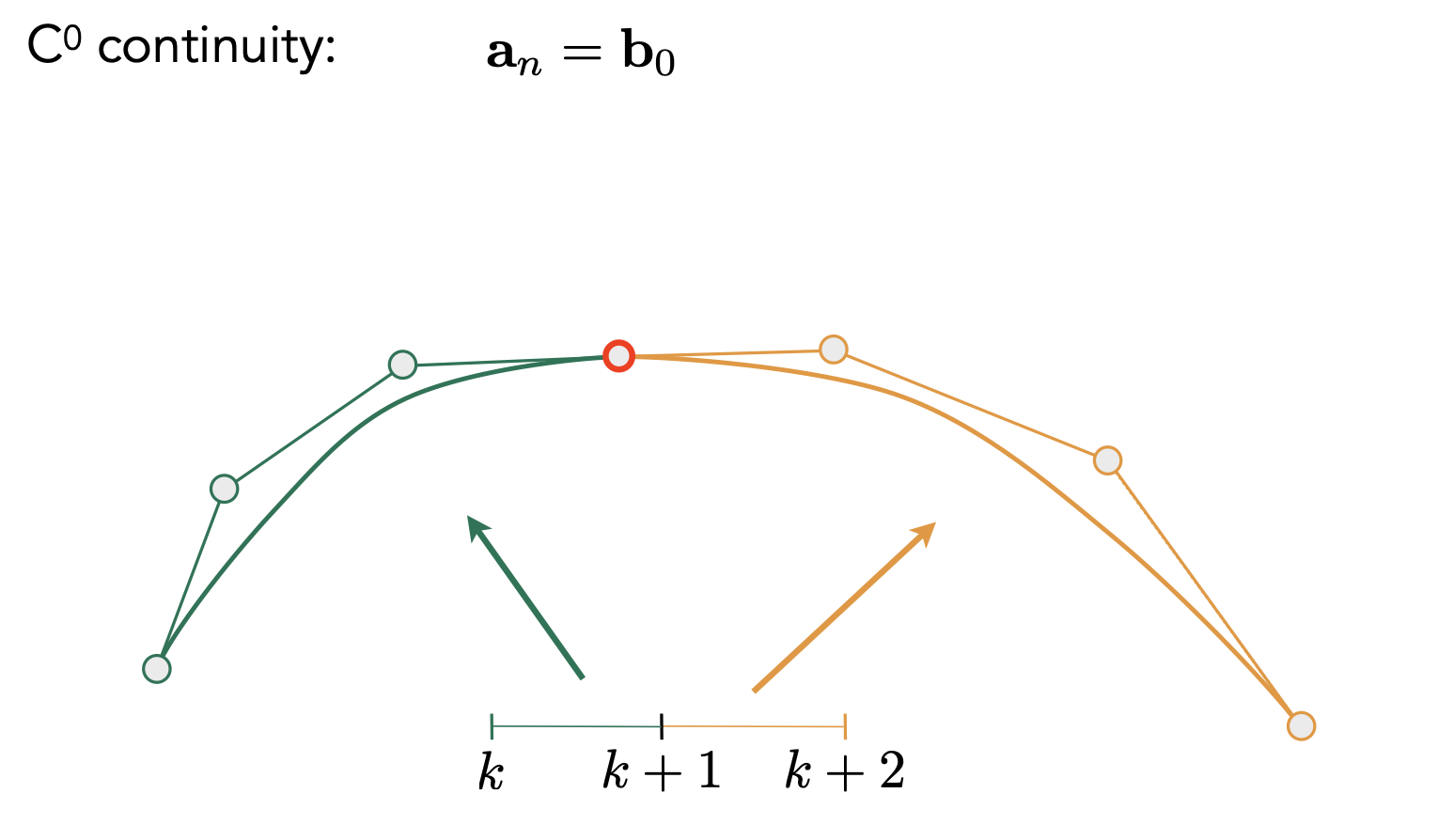
分段贝塞尔曲线的连续性: 连续表示 n 阶导连续

连续:
连续:
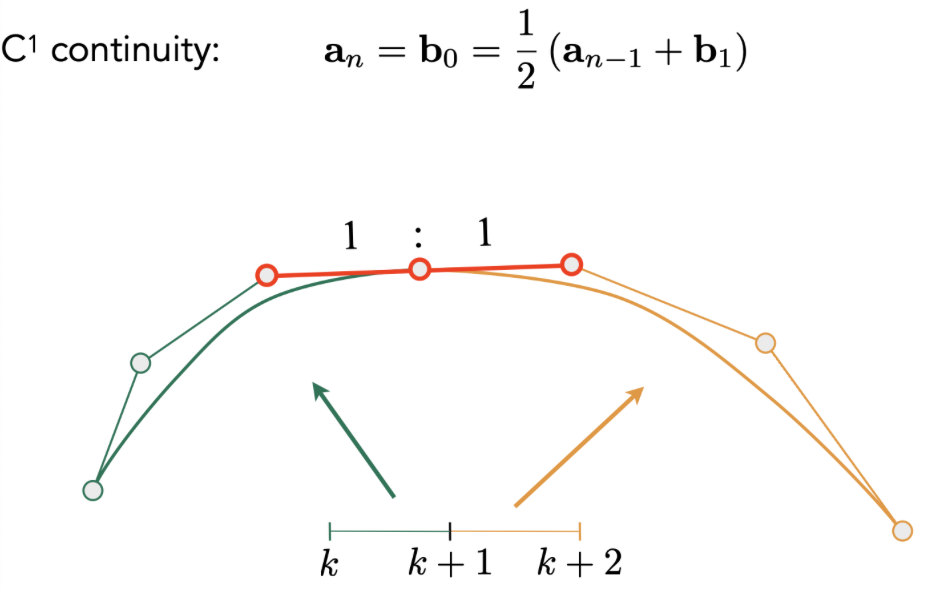
2 贝塞尔曲面
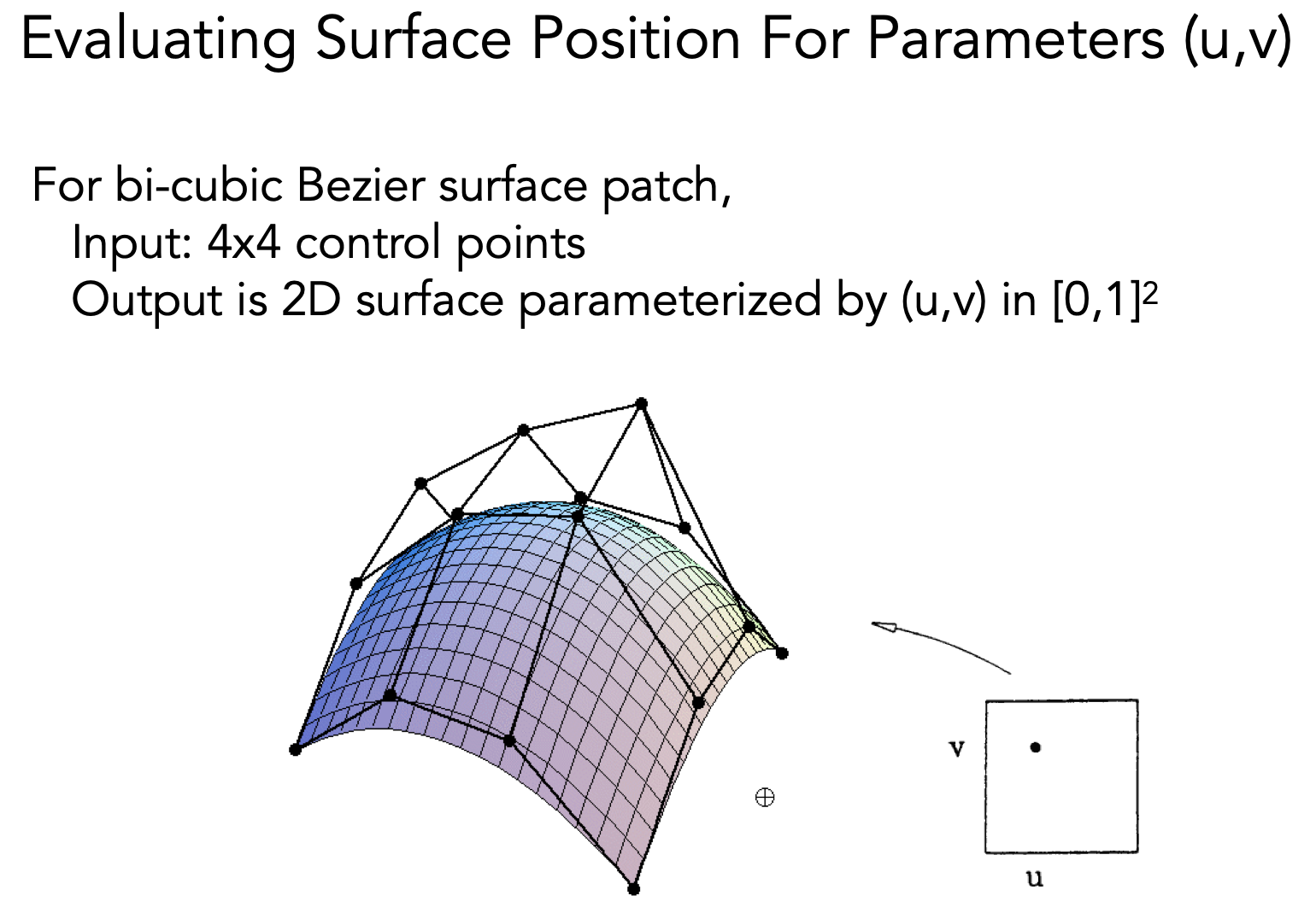
以 4*4 控制点的贝塞尔曲面为例:
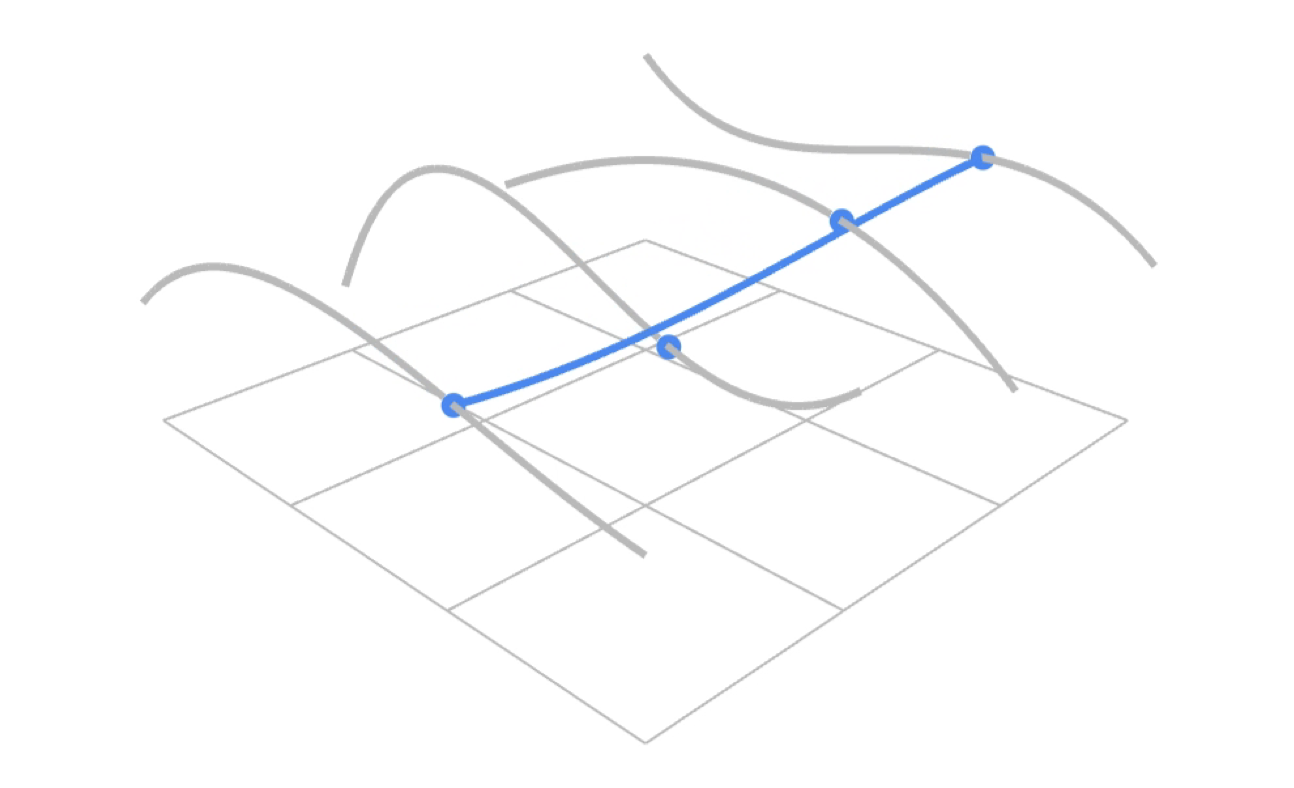
- 在这 4 个控制点之下利用第一个参数 u,运用计算贝塞尔曲线的方法得到蓝色点,因为有 4 列,所以一共可以得到如图所示的 4 个蓝色点。(灰色曲线分别为每列 4 个点所对应的贝塞尔曲线)
- 在得到 4 个蓝色顶点之后,在这四个蓝色顶点的基础之下利用第二个参数 v 便可以成功得出贝塞尔曲面上的正确一点
- 遍历所有的 u , v 值就可以成功得到一个贝塞尔曲面
Powered by Waline v2.15.5
