光线追踪(基本原理)
...约 731 字大约 2 分钟
光线追踪(基本原理)
Whitted-Style 光线追踪(Ray Tracing)
光线的定义:
- 直线传播
- 光线之间不会碰撞
- 光线从光源发出,进入场景不断碰撞,最终到达眼睛
1 光线投射(Ray Casting)
对每一个 pixel,从眼睛/相机发出一根光线,最终打到某一点,如果该点与物体相交,则表示能看到物体上的这个点。再让该点与光源作连线,如果没有遮挡则形成一条有效光路,否则为阴影。(这比 shadow mapping 更方便)

可以利用 Blinn-Phong 模型对这个点进行局部光照模型计算,得到该像素的颜色,那么遍历投影平面上的所有像素就能得到一张完整的图像。但如果光线追踪仅仅是在 Ray Casting 就停止的话,那么它的效果与局部光照模型是一样的,因此我们还需要考虑反射、折射。
2 递归光线追踪(Recursive Ray Tracing)
- primary ray:眼睛发出的光线
- secondary ray:经过反射或折射的光线
- shadow ray:交点到光源的连线
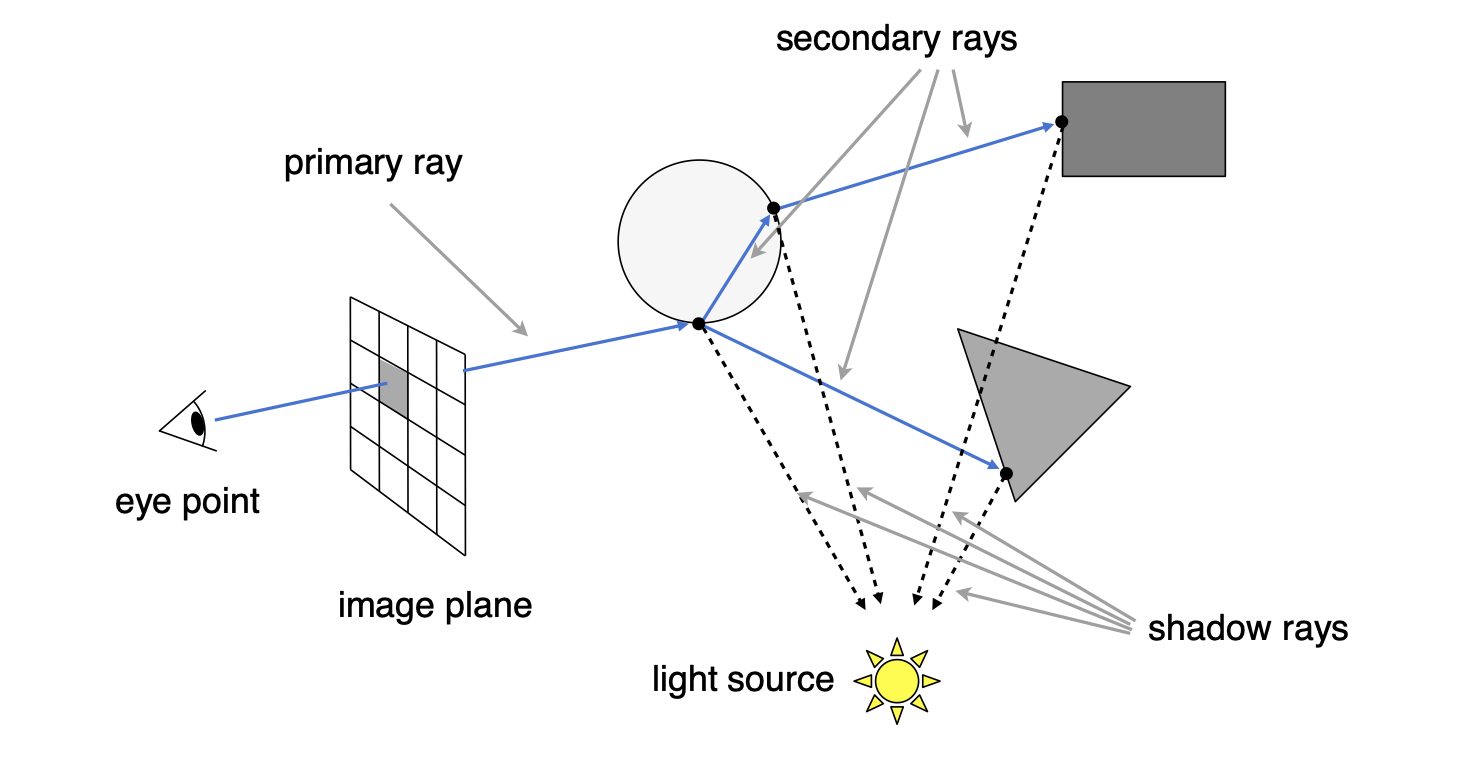
- 递归有个终止条件,不可能无限递归下去
- 光线在每次反射或者折射之后都有能量损耗,具体的在之后会讲解
- 如果光线没有碰撞到物体则返回一个背景色
3 射线方程(Ray Equation)
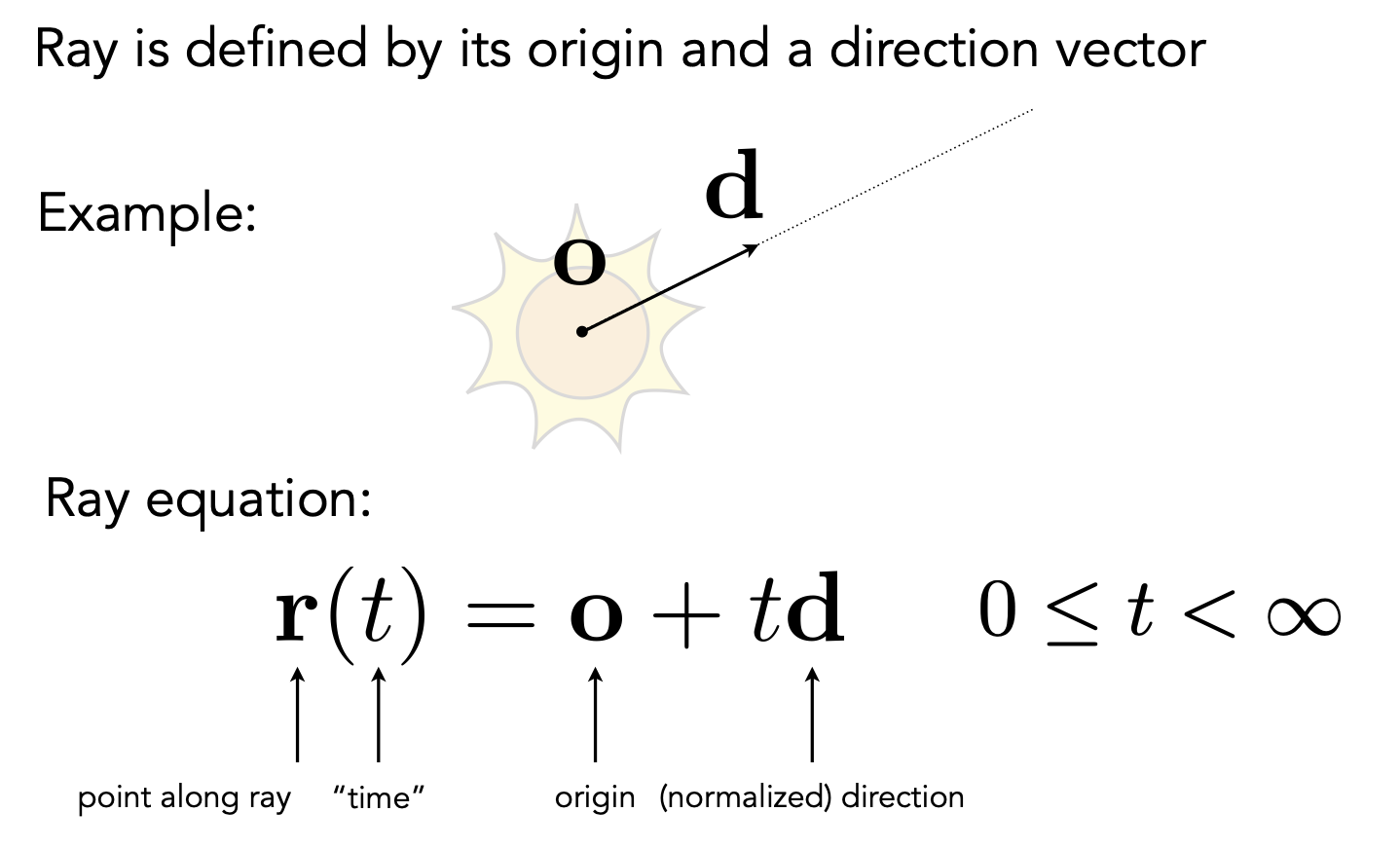
Ray 经过 t 时刻到达点 P 可以表示为 ,对于原公式中 r(t)=o+td,r 和 o 都是点,d 是方向向量。
4 光线与物体的交点
4.1 隐式几何
直接联立几何方程和射线方程,只取实数和正数作为结果

4.2 显式几何
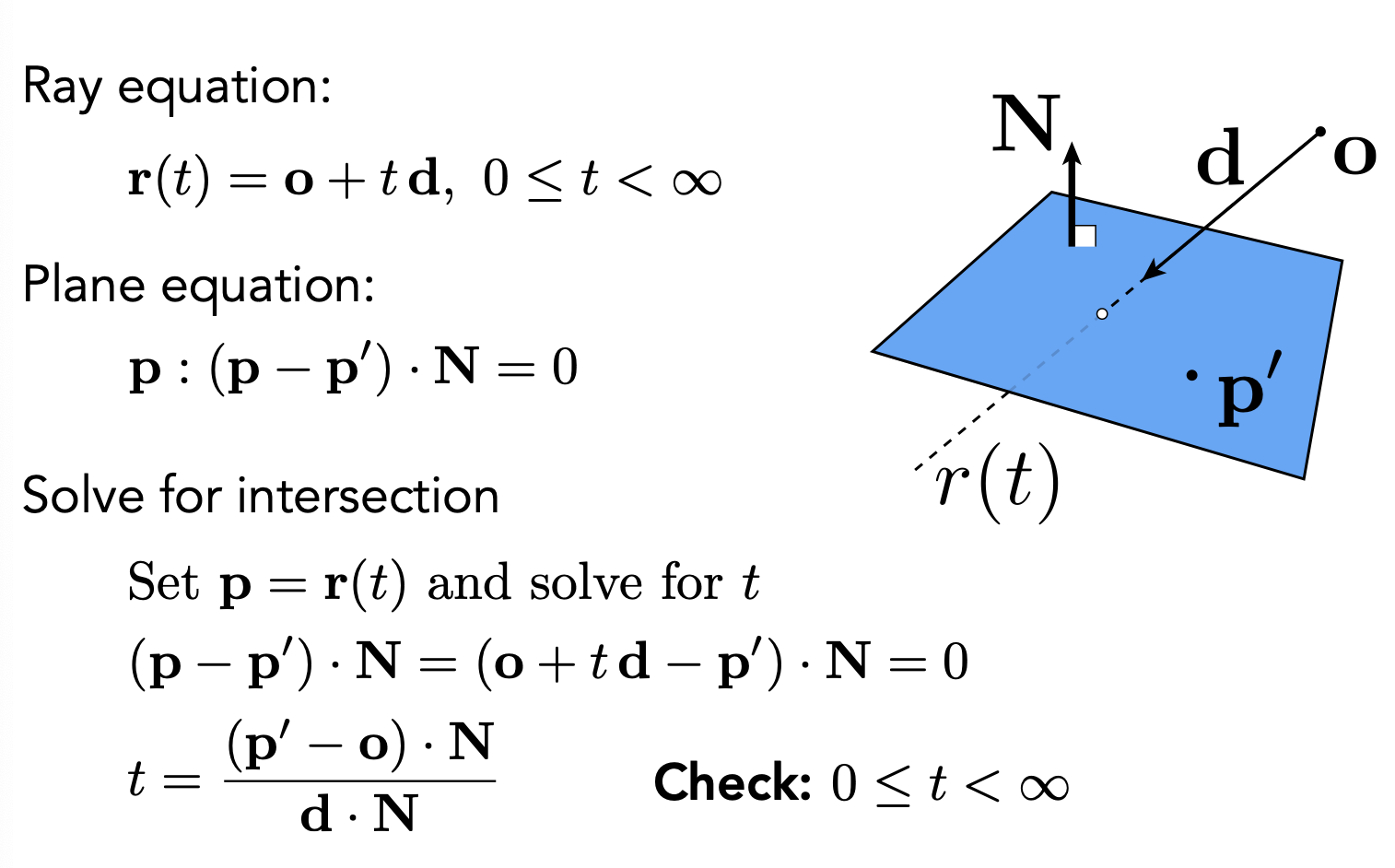
图形学中的模型通常由三角形的 mesh 组成,判断一条射线与显式曲面的交点,其实也就是计算光线与三角形面的交点。一个平面是由平面的法向量和平面上的一个点定义,可以通过下图的方程判断一个点是否在平面上。

然后再将射线方程代入平米方程即可解出 t
通过上述方法求出结果后还要通过向量叉乘的方法判断该点是否在三角形内部,还可以通过下图的方法在求出t的同时判断是否在三角形内部

该方法是基于重心坐标,通过克莱姆法则求解线性方程。因为是基于重心坐标来求解,所以只要 、、 三个数都 就可以知道该点是在三角形内部。
Powered by Waline v2.15.5
