SplattingAvatar-论文笔记

SplattingAvatar: Realistic Real-Time Human Avatars with Mesh-Embedded Gaussian Splatting

项目地址

CVPR 2024

Fig. 1: Overview

Abstract

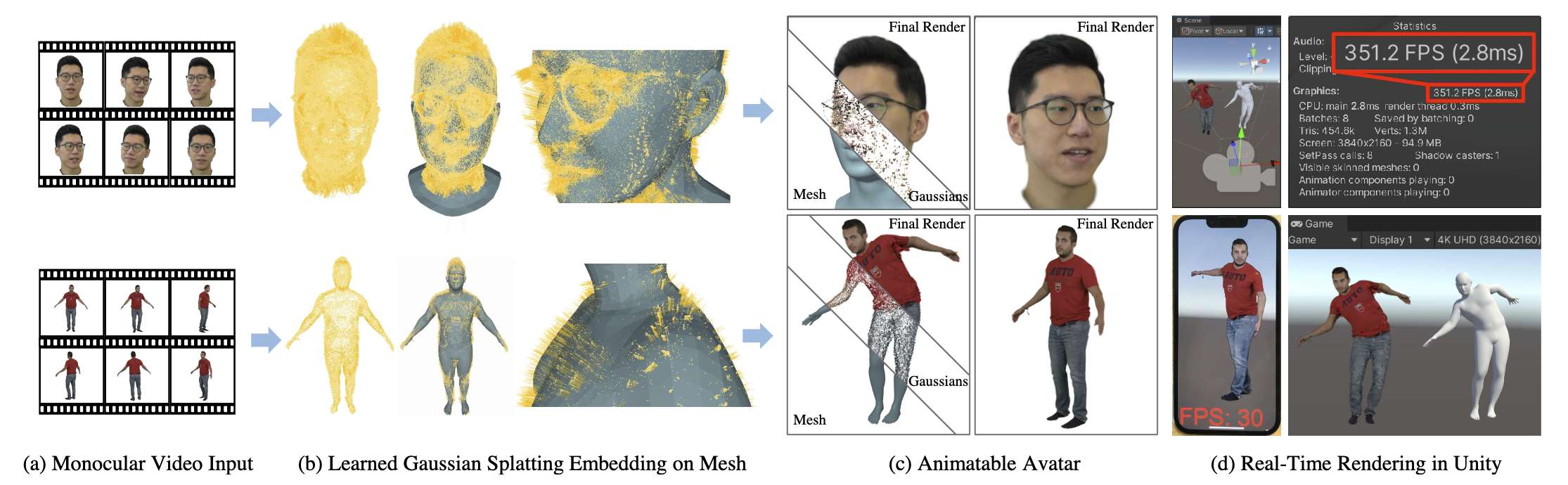
我们展示了 SplattingAvatar，这是一种在三角形网格上嵌入 3DGS 的逼真数字人的混合 3D 表现形式，在现代 GPU 上的渲染速度超过 300 FPS，在移动设备上的渲染速度为 30 FPS。我们通过显式网格和隐式高斯进行拼接建模，将数字人的运动和外观分离开来。高斯由三角形网格上的重心坐标和位移定义为 Phong Surface。我们通过改进 Lifted Optimiaztion 方法，在三角形网格上 walking 的同时优化高斯参数。SplattingAvatar 是数字人的混合表现形式，其中网格代表低频运动和表面变形，而高斯则代表高频几何和细节外观。现有的变形方法依赖于基于 MLP 的线性混合蒙皮 (LBS) 来表示运动，与之不同的是，我们直接通过网格来控制高斯的旋转和平移，这就增强了它与各种动画技术 (如骨骼动画、混合形状和网格编辑) 的兼容性。SplattingAvatar 可通过单目视频对全身和头部进行训练，在多个数据集上显示出一流的渲染质量。

Introduction

本文提出用可训练的 mesh 的 embedding 来显示控制高斯，将 mesh 表示为 Phong surface，embedding 表示为 $(k,u,v,d)$，其中 $(u,v)$ 表示第 $k$ 个 mesh 的重心坐标在 embedding 上的位置，$d$ 表示沿着法向量方向的位移。

本文的主要贡献：

• 本文介绍了一种将 3DGS 与 mesh 整合在一起的框架，它提供了一种新的数字人表现形式，既逼真又能提高计算效率。
• 本文使用 lifted optimization 来优化数字人模型，允许对高斯参数和 mesh embeddings 进行联合优化，以实现精确的重建。
• 本文通过综合评估和 Unity，展示了实时渲染的能力和创建各种数字人的泛化性。

Method

Fig. 2: Pipeline

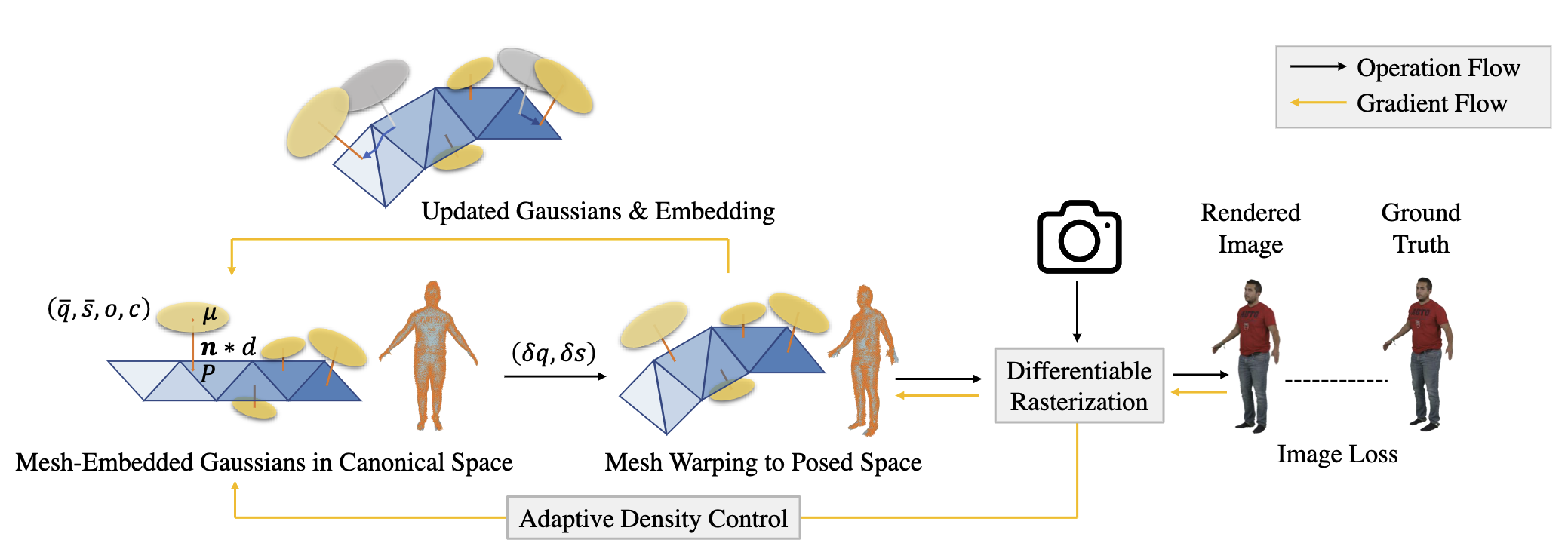
Overview

在单目图像序列中，每张图像都有一个 registered 的 mesh 模板，即 SMPLX 或 FLAME，本文将数字人混合表示为嵌入在 mesh 上的 3D 高斯。高斯的参数包括位置、旋转、比例、颜色和不透明度，它们是半透明的 3D 粒子，通过基于 splatting 的光栅化技术呈现在摄像机视图中。

每个 3D 高斯以其局部 $(u,v,d)$​ 坐标嵌入到标准 mesh 的一个三角形上。embedding 直接定义了高斯在标准空间和 pose 空间中的位置。除位置外，每个高斯都有自己的旋转、缩放、颜色和不透明度参数。当 mesh 通过动画变形时，embedding 也会为每个高斯提供额外的旋转和缩放参数。与姿势相关的额外旋转由每个顶点四元数的重心插值定义，而额外缩放则由嵌入三角形的面积变化定义。

在优化过程中，高斯参数和 embedding 参数同时更新。当 $(u,v)$​ 的更新使 embedding 跨越三角形边界时，重心会在邻近的三角形中重新计算，就像高斯在网格上行走一样。为了支持 embedding，本文调整了原版 3D 高斯的 clone 和 split 策略。

Embedding on mesh

Phong surface 把一个点的 position 和 normal 定义在三角形里。对于三角形 $k$ 上的点 $P$，重心坐标为 $(u,v)$，它的 position 和 normal 是三角形顶点 $\{V_1,V_2,V_3\}$ 和每个顶点的法向量 $\{n_1,n_2,n_3\}$ 的线性插值：

$$P=\mathcal{V}(k,u,v)=u\times V_1+v \times V_2+(1-u-v)\times V_3 \tag{1}$$

$$n=\mathcal{N}(k,u,v)=u\times n_1+v \times n_2+(1-u-v)\times n_3 \tag{2}$$

把高斯基元的位置即均值 $\mu$ 定义为点 $P$ 沿着法向量方向位移 $d$：

$$\mu=P+d\times n \tag{3}$$

把 embedding $E={k,u,v,d}$ 近似为 mesh 表面周围的一阶连续空间。

对于某一帧标准空间和 pose 空间中的三角形，根据三角形的切线、双切线 (bitangent) 和法线计算矩阵 $\{R_{cano}, R_{pose}\}$，求出三角形从标准空间到 pose 空间的旋转。然后将旋转矩阵转换为四元数，并根据周围邻近三角形的面积加权平均值计算每个顶点的四元数 $q_V$：

$$R_k=R_{cano}R^{-1}_{pose} \tag{4}$$

$$q_V = \frac{\sum_{k\in\Omega_V}A_kq_k}{\sum_{k\in\Omega_V}A_k} \tag{5}$$

• $\Omega_V$ 表示顶点 $V$ 的相邻三角形
• $A_k$ 和 $q_k$ 分别是三角形的面积和四元数

对于第 t 帧的 embedding $E_i$，将重心旋转插值四元数 $\delta_{q_{i,t}}$ 乘以标准空间的高斯的旋转四元数 $\bar{q}_i$，最后得到 $E_i$ 的旋转四元数 $q_{i,t}$：

$$\delta_{q_{i,t}}=u\times q_1+v\times q_2+(1-u-v)\times q_3 \tag{6}$$

$$q_{i,t}=\delta_{q_{i,t}}\times\bar{q}_i \tag{7}$$

• $\{q_1,q_2,q_3\}$ 表示 $E_i$​ 所在三角形三个顶点在第 $t$​ 帧的四元数

相同的操作也被用在缩放上，即用三角形的面积变化来表示变形引起的缩放：

$$s_{i,t}=(A_{pose}/A_{cano})\bar{s}_i \tag{8}$$

本文省略了原版 3DGS 中的球谐函数。

在标准空间的 mesh 上随机选取 10k 个三角形和重心坐标进行初始化，并将 $d$ 初始化为 $0$。高斯基元的位置通过 embedding 进行计算，其他属性还是和原版高斯一样。一开始高斯基元都在 mesh 的表面，随着训练的进行， embedding 会逐渐贴合几何表面，并且在纹理丰富的区域产生更多的高斯基元，图 3 展示了这个过程。

Fig. 3: 高斯 embedding 的变化过程。在表面以外的部分会有正的偏移量 (比如头发)，而其他区域，比如面部，则会有负偏移量，因为高斯基元位置的均值在 mesh 内部

Differentiable rendering of Gaussian Splatting

由于单目视频的视角和姿态变化有限，本文提出了一个缩放正则化项，以防止高斯球变长变细。最后的光度损失是 $\mathcal{L}_1$、感知损失 $\mathcal{L}_{lpips}$ 和缩放正则项 $\mathcal{L}_{scaling}$ 之和：

$$\mathcal{L}=\mathcal{L}_1+\lambda_1\mathcal{L}_{lpips}+\lambda_s\mathcal{L}_{scaling} \tag{9}$$

$$\mathcal{L}_{scaling}(i)= \begin{cases} |\hat{s_i}|, & \hat{s_i}>\max(T_s,T_r\check{s_i})\\ 0, &\text{otherwise } \end{cases} \tag{10}$$

• $s_i\in\R^3$ 表示高斯的缩放
• $\hat{s_i}$ 和 $\check{s_i}$​ 分别表示最大和最小的缩放值
• $T_s$ 和 $T_r$ 分别是缩放阈值和比例阈值

当 $\hat{s_i}$ 过长 (比 $T_s$ 大) 或过细 (比 $T_r \times \check{s_i}$​ 大) 的时候缩放正则项才会生效。

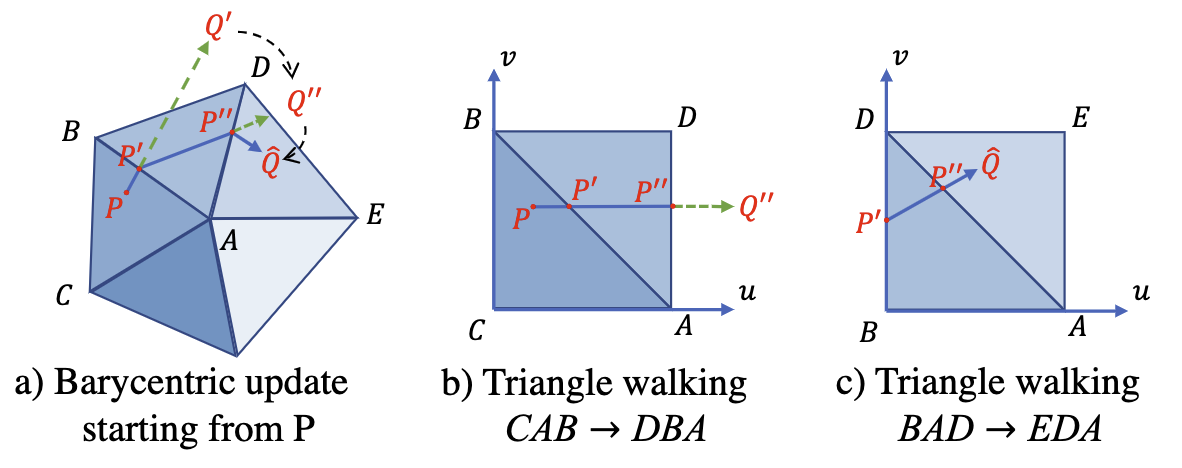
Walking on a triangle mesh

通过第 $k$ 个三角形定义点 $P$ 的重心坐标 $(k,u,v)$，当更新移动后的点 $Q=(k,u,v)+(\delta u,\delta v)$ 在第 $k$ 个三角形外，则在第 $k$ 个三角形和相邻第 $k'$ 个三角形共享的边上找一个点 $P'$，并把剩余的移动重新表示在第 $k'$ 个三角形内为 $Q'=P'+(\delta u'+\delta q')$。由于重心坐标与三角形的形状无关，在不失一般性的前提下，重新表示的方法是将两个相邻的三角形视为直角三角形，交点位于斜边上。更新会反复重新表示，直到在最终三角形内结束。整个过程如图 4 所示。

Fig. 4: Walking on triangles for embedding update

Reference:

[1]SplattingAvatar: Realistic Real-Time Human Avatars with Mesh-Embedded Gaussian Splatting

[2]The Phong Surface: Efficient 3D Model Fitting Using Lifted Optimization