LayGA-论文笔记

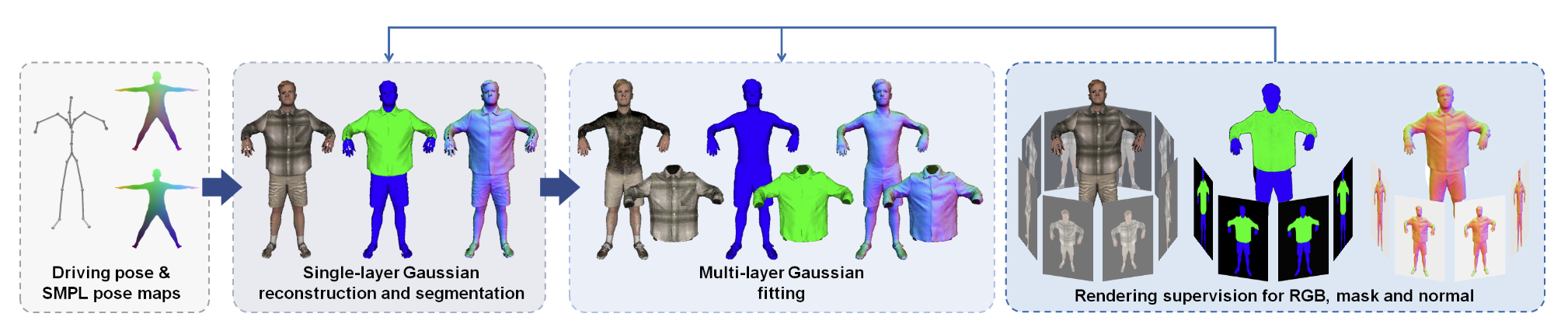
LayGA: Layered Gaussian Avatars for Animatable Clothing Transfer

项目地址

SIGGRAPH 2024

Fig. 1: Overview

Abstract

可动画服装转移，旨在不角色间转移服装并对服装进行动画，是一个具有挑战性的问题。大多数数字人工作将人体和服装的表示统一在一起，这导致在不同身份之间的虚拟试衣变得困难。更糟的是，统一的表示通常无法准确跟踪服装的滑动。为了解决这些限制，本文提出了分层高斯数字人 (Layered Gaussian Avatars, LayGA)，这是一种新的表示方法，将身体和服装分为两个独立的层，用于从多视角视频中实现逼真的可动画服装转移。本文的表示方法基于高斯图数字人，因为它在服装细节的表示能力上非常出色。然而，高斯图会在实际表面周围产生非结构化的 3D 高斯分布。缺乏平滑的显式表面在准确的服装跟踪和处理身体与服装之间的碰撞时带来了挑战。因此，本文提出了两阶段训练方法，包括单层重建和多层拟合。在单层重建阶段，本文提出了一系列几何约束来重建平滑表面，同时获得身体和服装之间的分割。接下来，在多层拟合阶段，本文训练两个独立的模型来表示身体和服装，并利用重建的服装几何形状作为三维监督，以实现更准确的服装跟踪。此外，本文提出了几何和渲染层，用于高质量的几何重建和高保真渲染。总体而言，LayGA 实现了逼真的动画和虚拟试穿，并优于其他 baseline 方法。

Introduction

本文将身体和服装分为两个独立的层，但是直接学习两组高斯来分别表示身体和衣服是不可行的。因为 3DGS 通常在表面上分布不均匀，无法为区分出人体和衣服，而这对于服装适应不同体型和处理衣服和人体的碰撞是很重要的。因此本文提出了两阶段训练方法，包括单层重建和多层拟合。在单层重建阶段，提出了一系列的几何约束来强制 3D 高斯生成在平滑的表面上。最后还提出额外的渲染层来保证平滑重建的同时实现高保真的渲染，因为通过几何约束获得的平滑表面可能会限制渲染的质量。

本文的创新点：

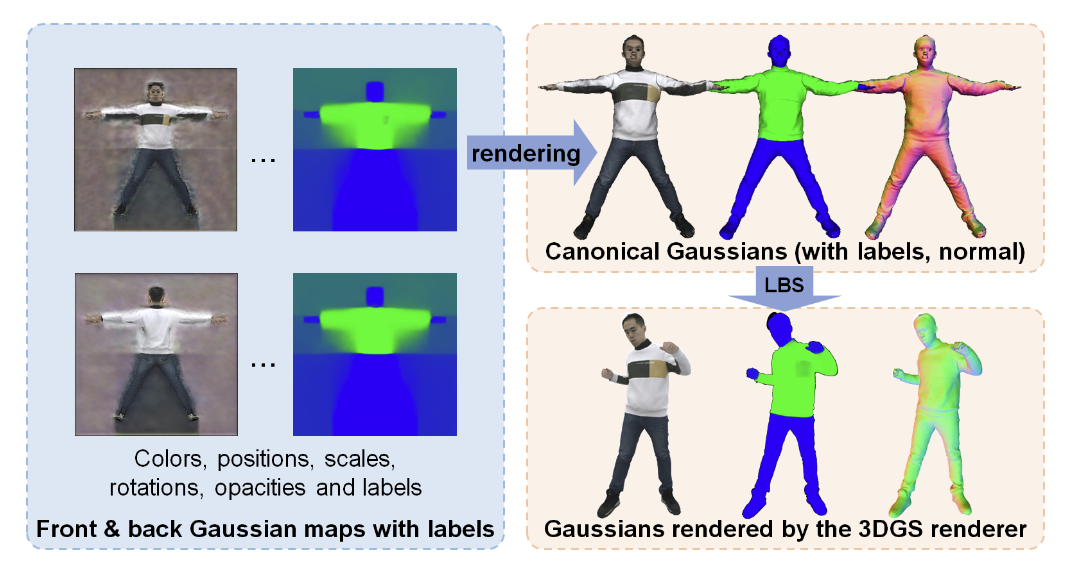
• 提出了分层高斯数字人 (LayGA)，这是首个基于 3DGS 的分层数字人表示法，用于可动画的服装转移。
• 在 3D 高斯上引入了几何约束，以实现平滑的表面重建，并支持在分层表示中处理人体与服装之间的碰撞。
• 在多层学习中，引入了先前的衣服的分割作为监督，以便更准确地跟踪服装边界。此外，还引入了一个渲染层，以缓解几何限制带来的渲染质量下降问题。

Method

Fig. 2: Pipeline

Clothing-aware Avatar Representation

Fig. 3: Illustration of the clothing-aware avatar representation

这篇文章是基于 Animatable Gaussians 做的，通过预测二维的 pose 相关高斯图来创建高保真的数字人。本文的服装感知数字人表示 (图 3) 就是在其 pose 相关高斯图上对做了针对性修改。

先学习 position map，然后再用 StyleUNet 学习 Gaussian map 的过程和 Animatable Gaussians 是一样的，这篇文章的创新是除了高斯的基本参数外，额外多学习一个 label 用来区分这个高斯是属于身体还是衣服。

本文的高斯参数为：

• $c_i\in\R^3$ 表示颜色
• $\Delta\bar{x}_i\in\R^3$ 表示参数化模板上的点的 offset
• $o_i\in\R$ 不透明度
• $\bar{s}_i\in\R^3$ 表示缩放向量
• $\bar{q}_i\in\R^4$ 表示选择四元数
• $p_i^{cloth}$ 和 $p_i^{body}$ 分别表示高斯属于衣服或者身体的概率

最终 3D 高斯的均值和协方差为：

$$\bar{x}_i=\bar{x}_i^{smpl}+\Delta\bar{x}_i \tag{1}$$

• $\bar{x}_i^{smpl}$ 表示像素 $i$ 所对应的参数化模板上的点

$$x_i=R_i(\theta)\bar{x}_i+t_i(\theta) \tag{2}$$

$$\Sigma_i=R_i(\theta)\bar{\Sigma}_iR_i(\theta)^T \tag{3}$$

• $R(\theta)$ 和 $t(\theta)$ 表示通过 pose 参数 $\theta$ 求出来的 LBS 变换矩阵
• $\bar{\Sigma}_i$ 表示通过 $\bar{s}_i$ 和 $\bar{q}_i$ 算出来的标准空间下的协方差矩阵

Single-Layer Modeling with Geometric Constraints

在单层重建阶段，目标是训练一个模型，生成平滑分布在人体实际几何表面上的 3D 高斯，并同时获得人体和衣服之间的分割。

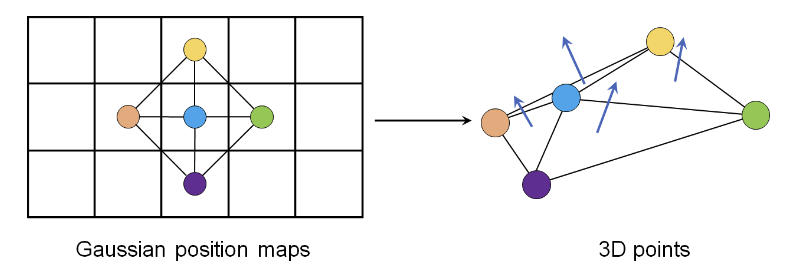
Geometric Constraints for Reconstruction

本文希望重建的穿衣人体表面是连续、平滑的，具有服装细节和清晰的服装边界。通过 2D 高斯图上均匀分布的像素映射为 3D 高斯 ，因此可以方便地使用每个像素的邻域来约束底层几何。具体来说，本文通过一些几何约束来正则化并提高细节。

Image-based Normal Loss. 使用法向量作为额外的监督信号，使用图片中的像素和其相邻像素来获取法向量。如图 4 所示，对于每个像素 $i$，假设其相邻像素分布为 $j,k,l,m$ (逆时针排序)，法向量 $n_i$ 为：

$$n_i= R_i(\theta) \bar{n}_i /\left\|R_i(\theta) \bar{n}_i\right\|_2, \quad \bar{n}_i=\hat{n}_i /\left\|\hat{n}_i\right\|_2 \\ \tag{4}$$

$$\hat{n}_i=\left(\bar{x}_j-\bar{x}_i\right) \times\left(\bar{x}_k-\bar{x}_i\right)+\left(\bar{x}_k-\bar{x}_i\right) \times\left(\bar{x}_l-\bar{x}_i\right)\\ +\left(\bar{x}_l-\bar{x}_i\right) \times\left(\bar{x}_m-\bar{x}_i\right)+\left(\bar{x}_m-\bar{x}_i\right) \times\left(\bar{x}_j-\bar{x}_i\right) \tag{5}$$

• $\bar{x}_i$ 表示像素 $i$ 的坐标

$\hat{n}_i$ 其实就是相邻 4 个平面法向量的矢量和，$\bar{n}_i$ 就是进行单位化，最后的 $n_i$ 是将该法向量从标准空间变换到观测空间

当计算法向量时，只考虑向量像素都在模版内的像素点。最终的 $\mathcal{L}_{norml}$ 是对渲染出来的法向量图和通过 RGB 图预测出来的法向量图之间求 $L_1$ loss。

Fig. 4: Illustration of normal computation on the Gaussian map

Stitching Loss. 由于本文的 3D 高斯是在两个独立的 map 上进行参数化的，因此引入了 $\mathcal{L}_{stitch}$，即 front map 中边界像素与 back map 中对应像素之间的 $L_2$ 损失，以防止不连续性。

Regularization. 和 Animatable Gaussians 一样加了一个 offset 正则化损失 $\mathcal{L}_{off}=\frac{1}{N}\sum_i||\Delta\bar{x}||_2^2$。还加了一个总变化 (total variational, TV) 损失 $\mathcal{L}_{TV}$，具体来说就是所有相邻像素之间的位置 $L_2$ 范数的均值，用于约束相邻两个像素之间的距离，防止 3D 高斯过于分散。使用边缘正则化损失 $L_{edge}$ 来正则化基本 SMPL-X 模型和变形模型之间的边长度。边是指两个相邻有效像素之间的边。$L_{edge}$ 是添加 offset 前后边长度的平均 $𝐿_2$ 损失。

最终几何损失函数为：

$$\mathcal{L}_{reg}=\lambda_{off}\mathcal{L}_{off}+\lambda_{TV}\mathcal{L}_{TV}+\lambda_{edge}\mathcal{L}_{edge}\\ \mathcal{L}_{geom}=\lambda_{normal} \mathcal{L}_{normal}+\lambda_{stitch} \mathcal{L}_{stitch}+\mathcal{L}_{reg} \tag{6}$$

Clothing Segmentation

上文提到会学习一个 label 用来区分这个高斯是属于身体还是衣服，即预测概率 $p_i^{body}$ 和 $p_i^{cloth}$ 来判断这个高斯基元是属于身体或者衣服。会用 3DGS 的渲染器将这两个值渲染为双通道的分割图像 $S$ (通道 $S^{body}$ 和 $S^{cloth}$)，label loss $\mathcal{L}_{label}$ 是渲染分割图 $S$ 和 GT $S_{gt}$ 之间的交叉熵损失：

$$\begin{aligned} \mathcal{L}_{ {label }}= & -\frac{1}{N_{ {body }}} \sum_i \log \left(S_i^{ {body }}\right)-\frac{1}{N_{ {cloth }}} \sum_{i^{\prime}} \log \left(S_{i^{\prime}}^{ {cloth }}\right) \\ & -\frac{1}{N_{ {bg }}} \sum_{i^{\prime \prime}} \log \left(1-S_{i^{\prime \prime}}^{ {body }}-S_{i^{\prime \prime}}^{ {cloth }}\right) \end{aligned} \tag{7}$$

• $i,i',i''$ 分别表示 $S_{gt}$ 中被分割为身体、衣服和背景的像素
• $N_{body},N_{cloth},N_{bg}$ 分别表示对应种类的像素的数量
• $S_{gt}$ 是综合考虑 SCHP 的和数据集自带的二进制 mask 之后的结果，具体规则如下
  • 如果像素的值在数据集自带的二进制 mask 中是无效的，则它被视为背景；
  • 如果像素被 SCHP 标记为背景，则被视为未确定；
  • 如果像素被 SCHP 标记为非上衣，则被视为身体；
  • 否则，该像素被视为服装；

和几何约束一样，也对 Gaussian label map 加了一个 $L_1$ TV loss $\mathcal{L}_{TV}^{label}$，对边界像素加了一个 $\mathcal{L}_{stitch}^{label}$，最终分割损失函数为：

$$\mathcal{L}_{ {seg }}=\lambda_{ {label }} \mathcal{L}_{ {label }}+\lambda_{\mathrm{TV}}^{ {label }} \mathcal{L}_{\mathrm{TV}}^{ {label }}+\lambda_{ {stitch }}^{ {label }} \mathcal{L}_{ {stitch }}^{ {label }} \tag{8}$$

渲染损失函数为：

$$\mathcal{L}_{ {render }}=\lambda_{\mathrm{L} 1} \mathcal{L}_{\mathrm{L} 1}+\lambda_{ {ssim }} \mathcal{L}_{ {ssim }}+\lambda_{ {lpips }} \mathcal{L}_{ {lpips }} \tag{9}$$

最后总的损失函数为：

$$\mathcal{L}=\mathcal{L}_{render}+\mathcal{L}_{geom}+\mathcal{L}_{seg} \tag{10}$$

Avatar Fitting with Multi-Layer Gaussian

多层建模阶段的目标是使用单层阶段分割出来的衣服的几何来构建双层的数字人。分割的标准是 $p^{cloth}>0.5$ 则被认为是衣服，其他的认为是身体。本节的模型架构和单层阶段类似，但做了部分的改变。

Separating Geometry and Rendering Layers

前文中加了几何约束来使 3D 高斯汇聚成一个平滑的表面，但是这些几何限制对 3DGS 的渲染质量产生了负面影响，可能是因为这些几何限制降低了高斯在高保真外观建模方面的灵活性。为了降低这些负面影响并保持光滑的几何表面，本文提出将几何层和渲染层分开。如图 5 所示，除了前面提到的 $\Delta\bar{x}_i$，还额外添加了一个 offset $\Delta\bar{y}_i$。高斯的位置属性只用第一个 offset 进行计算 (公式 1 和 2)，即几何层。高斯的位置加上额外的 offset 用于本阶段最终的渲染，即渲染层：

$$y_i=R_i(\theta)(\bar{x}_i^{smpl}+\Delta\bar{x}_i+\Delta\bar{y}_i)+t_i(\theta) \tag{11}$$

Fig. 5: Illustration of geometric and rendering layers. 𝜖 is the threshold for handling collisions.

为了约束身体层使其位于衣服层的里面，在身体几何层和衣服几何层之间施加了一个碰撞损失：

$$\mathcal{L}_{coll}=\frac{1}{N_{cloth}}\sum_i\max(\epsilon-d_i,0)^2,\ \text{where} \ \ d_i=(\bar{x}_i^{cloth}-\bar{x}_i^{body})\cdot\bar{n}_i^{body} \tag{12}$$

• $\epsilon$ 表示距离阈值
• $i$ 表示 clothing Gaussian map 中所有有效的像素

只是处理身体几何层和衣服几何层之间的碰撞无法保证对应的渲染层之间没有碰撞，因此对渲染层增加一个约束，确保渲染层贴近几何层：

$$\begin{aligned} \mathcal{L}_{ {layer }}= & \frac{1}{N_{ {body }}} \sum_i \max \left(\left\|\Delta \bar{y}_i^{ {body }}\right\|_2-\epsilon / 2,0\right)^2 \\ & +\frac{1}{N_{ {cloth }}} \sum_{i^{\prime}} \max \left(\left\|\Delta \bar{y}_{i^{\prime}}^{ {cloth }}\right\|_2-\epsilon / 2,0\right)^2 . \end{aligned} \tag{13}$$

$\mathcal{L}_{coll}$ 可以使服装几何层和人体几何层至少相距 $\epsilon$，而 $\mathcal{L}_{cloth}$ 使对应的渲染层最多相距 $\epsilon/2$，因此这两种损失函数会将两个渲染层拉开，避免碰撞。

Geometric Supervision from Reconstructions

由于仅使用图像监督来跟踪服装边界比较困难，因此本文在这一阶段通过在服装几何层和分割后的服装重建之间使用倒角距离 (Chamfer distance, CD) 损失来直接监督服装的运动：

$$\mathcal{cd}=\text{ChamferDist}(\{x_i^{cloth}\}_i,\{x_i^{recon}\}_i) \tag{14}$$

• $\{x_i^{cloth}\}_i,\{x_i^{recon}\}_i$ 分别表示衣服几何层的点云和第一阶段重建的点云

Segmentation Loss

在本阶段，分割的概率会直接设置为 $1$ 或 $0$，并且只保留 $\mathcal{L}_{reg}$ 中的 $\mathcal{L}_{label}$。最终本阶段的损失函数为：

$$\mathcal{L}=\mathcal{L}_{ {render }}+\mathcal{L}_{ {geom }}+\lambda_{ {label }} \mathcal{L}_{ {label }}+\lambda_{ {coll }} \mathcal{L}_{ {coll }}+\lambda_{ {layer }} \mathcal{L}_{ {layer }}+\lambda_{ {cd }} \mathcal{L}_{\mathrm{cd}} \tag{15}$$

Todo

本文最后还有一个 Animatable Clothing Transfer and Collision Handling 章节，用于在不同角色之间转移服装并处理碰撞，暂时先跳过。

Reference

[1]LayGA: Layered Gaussian Avatars for Animatable Clothing Transfer