Animatable Gaussians-论文笔记

Animatable Gaussians: Learning Pose-dependent Gaussian Maps for High-fidelity Human Avatar Modeling

项目地址

CVPR 2024

Fig. 1: Overview

Abstract

从 RGB 视频中建立可动画化的数字人模型是一个长期存在且极具挑战性的问题。最近的研究通常采用基于 MLP 的神经辐射场（NeRF）来表示三维人体，但纯 MLP 仍然难以回归与姿势相关的服装细节。为此，我们引入了动画高斯，这是一种新的数字人表示方法，它利用强大的 2D CNN 和 3DGS 来创建高保真数字人。为了将 3DGS 与可动画化的数字人联系起来，我们从输入视频中学习参数模板，然后将模板参数化为正面和反面的标准空间的高斯图，其中每个像素代表一个高斯基元。学习到的模板对穿着的服装具有自适应性，可用于制作连衣裙等宽松服装的模型。这种以模板为导向的二维参数化使我们能够采用功能强大的基于 StyleGAN 的 CNN 来学习与姿势相关的高斯图，从而为详细的动态外观建模。此外，我们还引入了一种姿势投影策略，以更好地泛化新姿势。总之，我们的方法可以创建具有动态、逼真和泛化外观的逼真数字人。实验表明，我们的方法优于其他最先进的方法。

Introduction

本文的贡献：

• 一种新的数字人表示法，它在数字人建模中引入了显示的 3DGS 技术，利用功能强大的 2D CNN 创建具有高保真姿态动态特性的逼真数字人。
• 模板指导参数化，可为一般服装（如连衣裙）学习特定特诊模板，并将 3D 高斯参数化为正反高斯图，以便与二维网络兼容。
• 一种简单而有效的姿态投影策略，在驱动信号上使用 PCA，对新姿态具有更好的泛化能力。

Method

Fig. 2: Pipeline

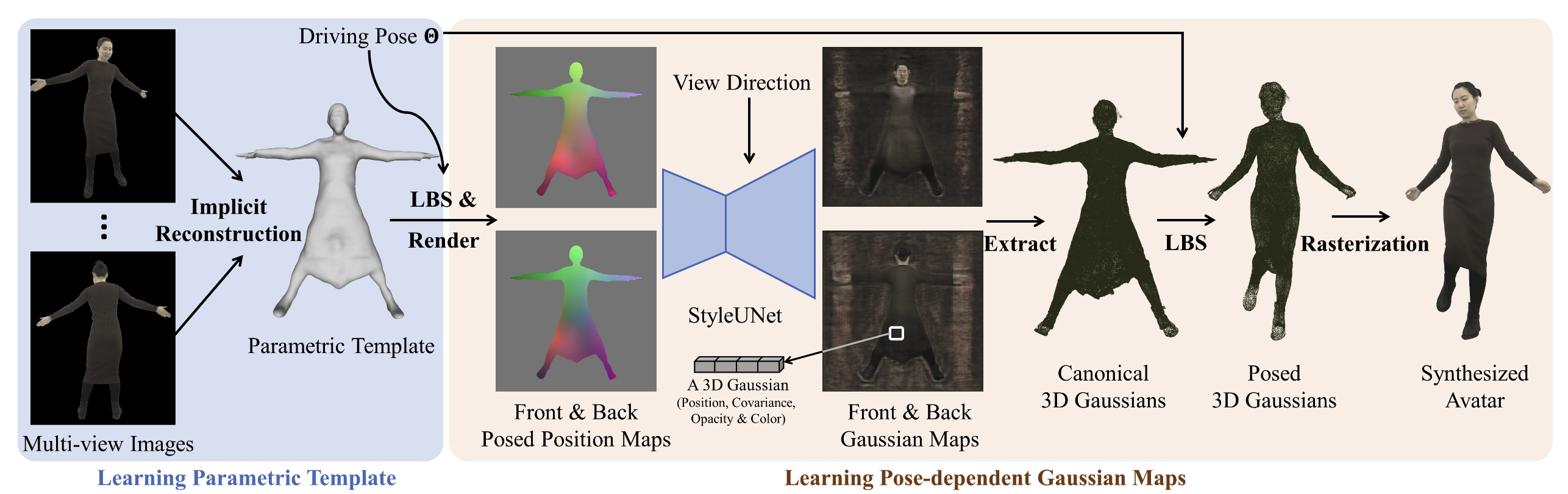
Overview

输入为 RGB 视频，以及每一帧的 SMPL-X 的 pose 和 shape 参数。

1. Learning Parametric Template：从输入视频中挑选一帧接近 A-pose 的图像，然后通过 SMPL 蒙皮和基于 SDF 的体渲染来优化一个标准空间 SDF 和颜色场。通过 Marching Cubes 从标准空间 SDF 中提取模板 mesh。最后，将蒙皮权重从 SMPL 顶点扩散到模板表面，得到一个可变形参数模板。
2. Learning Pose-dependent Gaussian Maps：给定一个训练 pose 后，我们首先通过线性混合蒙皮（LBS）将模板变形到 pose 空间，然后将 pose 顶点坐标渲染到标准空间的正反视图上，从而得到两个位置图。位置图作为 pose 条件，并通过 StyleUNet 转换为正反高斯图。然后，我们在模板 mask 内提取有效的 3D 高斯图，并通过 LBS 将标准空间 3D 高斯变形到 pose 空间。最后，我们通过可微光栅化技术，将 pose 空间的 3D 高斯渲染到给定的相机空间中。

Avatar Representation

Learning Parametric Template：这一部分的目的是从多视角图片中重建出标准空间中的几何模型作为模板。首先将标准空间的模板用 SDF 和 颜色场来表示。为了将标准空间变换到 pose 空间，先用扩散蒙皮权重的方法预计算出准空间中的蒙皮权重体积 $\mathcal{W}$​。扩散蒙皮权重通过沿着 SMPL 表面的法线方向，将权重从 SMPL 表面扩撒到整个 3D 空间。对于 pose 空间中的一个点，用 root finding 的方法 (公式 1) 找到其在标准空间中的对应点。

$$\min_{\mathbf{x}_c}||\mathrm{LBS}(\mathbf{x}_c;\Theta,\mathcal{W})-\mathbf{x}_p||_2^2 \tag{1}$$

• $\mathrm{LBS}(\cdot)$ 是将标准空间中的点转换到 pose 空间的混合蒙皮函数
• $\mathbf{x}_c$ 和 $\mathbf{x}_p$ 分别表示标准空间中的点和其在 pose 空间对应的点
• $\Theta$​ 表示 SMPL 的 pose 参数

找到标准空间中的对应点后，查询该点的 SDF 和颜色，通过基于 SDF 的体渲染方法来渲染 RGB 图像。将渲染图像和 GT 之间进行比较来优化标准空间的 SDF。最后从 SDF 中提取出几何模板，并且通过预计算的权重体积 $\mathcal{W}$​ 查询每个顶点的蒙皮权重来获取可变形参数化模板。

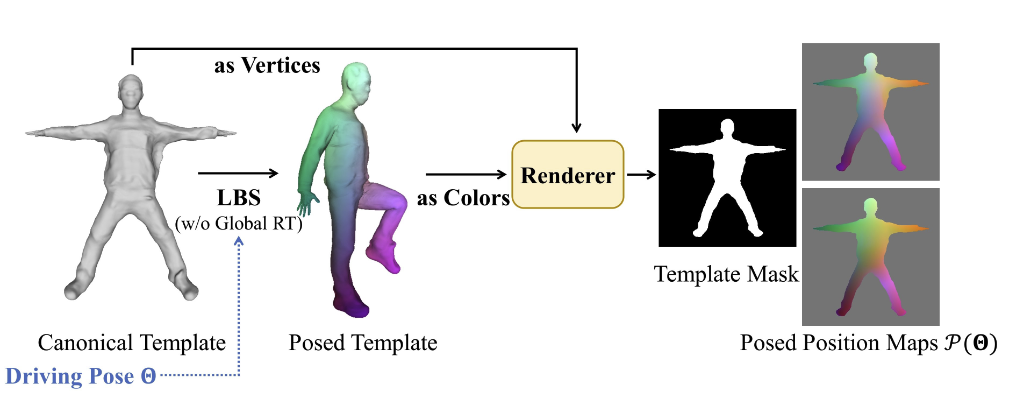
Template-guided Parameterization：这一部分的目的是获取 posed position maps。用 2D CNN 取代 MLP 来获取更高质量的数字人，首先需要将 3D 表示的数字人参数化到 2D 空间。本文提出通过正交投影到方法，把 3D 高斯参数化为正反 2 个 posed position maps，投影的过程如图 3 所示。要用 2D 图像来表示 3D 信息，一个很好的解决方法就是用颜色来表示第三维。首先将参数化模板通过 LBS 变形到 pose 空间，用标准空间中的顶点和其对应 pose 空间顶点的颜色，然后用正交投影的方式渲染成正反 2 个 posed position maps $\mathcal{P}_f(\Theta)$ 和 $\mathcal{P}_b(\Theta)$，作为网络的 pose 条件。

Fig. 3: Posed Position Maps

Pose-dependent Gaussian Maps：使用 StyleUNet $\mathcal{F}$ 通过 pose 条件来预测正反高斯图 $\mathcal{G}_f(\Theta)$ 和 $\mathcal{G}_b(\Theta)$

$$\mathcal{G}_f(\Theta),\mathcal{G}_b(\Theta)=\mathcal{F}(\mathcal{P}_f(\Theta),\mathcal{P}_b(\Theta),\mathcal{V}) \tag{2}$$

高斯图的每个像素表示一个包含位置、协方差、不透明度和颜色信息的 3D 高斯。本文还利用视角方向图 $\mathcal{V}$​ 约束高斯图，以模拟视角相关的差异。

LBS of 3D Gaussians：

$$\mathbf{p}_p=\mathbf{R}\mathbf{p}_c+\mathbf{t}\\ \Sigma_p=\mathbf{R}\Sigma_c\mathbf{R}^\top \tag{3}$$

• $\mathbf{p}_p$ 和 $\mathbf{p}_c$ 分别表示高斯基元在 pose 空间和标准空间的位置
• $\Sigma_p$ 和 $\Sigma_c$ 分别表示高斯基元在 pose 空间和标准空间的协方差
• $\mathbf{R}$ 和 $\mathbf{t}$ 分别表示每个高斯基元的选择矩阵和位移向量

Training：本文训练的时候是在参数模板上预测一个位移 $\Delta\mathcal{O}(\Theta)$ 来确保预测的高斯图的位置属性接近标准空间下的人体，而不是在 position map 上加。并且对其进行正则化 $\mathcal{L}_{reg}=||\Delta\mathcal{O}(\Theta)||_2^2$ 防止位移过大。本文的 loss 函数如下：

$$\mathcal{L}=\mathcal{L}_1+\lambda_{perceptual}\mathcal{L}_{perceptual}+\lambda_{reg}\mathcal{L}_{reg} \tag{4}$$

个人理解这个位移就是 SMPL 中的 Pose Blend Shapes，改变了 pose 后，首先要对标准空间的平均模板增加一个位移。

Pose Projection Strategy：首先提取出 posed position maps 中有价值的点，把他们 concatenate 成一个向量 $\mathbf{x}_t \in \R^{3M}$ ($M$ 是点的数量)。T 帧训练图像组成一个矩阵 $\mathbf{X}=[\mathbf{x}_1,\dots,\mathbf{x}_T]$ ，对 $\mathbf{X}$ 采用 PCA 获得 N 个主成分 $\mathbf{S}=[\mathbf{s}_1,\dots,\mathbf{s}_n] \in \R^{3M\times N}$，以及各成分的标准差 $\sigma_i$。给定新的 pose 生成的 posed position maps，将相应的特征 $\mathbf{x}$ 投影到 PCA 空间中：

$$\beta=\mathbf{S}^\top\cdot(\mathbf{x}-\bar{\mathbf{x}}) \tag{5}$$

• $\bar{\mathbf{x}}$ 是 $\mathbf{X}$ 的均值

然后用低维系数 $\beta$ 来重建 position：

$$\mathbf{x}_{recon}=\mathbf{S}\cdot\beta+\bar{\mathbf{x}} \tag{6}$$

最后将 $\mathbf{x}_{recon}$ reshape 成 $M\times3$ 的 tensor，并将其分散到 posed position maps 上。为了使重建的 position maps 位于训练姿态的分布中，本文将 $\beta$ 约束在 $[-2\sigma_i,2\sigma_i]$ 范围内。

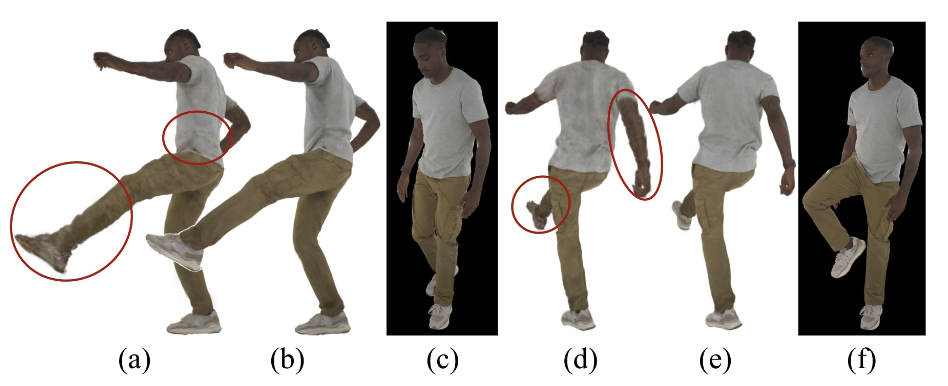
Pose Projection Strategy 的消融实验如图 4 所示。

本文用 PCA 的方法是为了将没见过的 pose 投影到训练集的空间里去，先把 pose map 映射到 PCA 空间，再重建回去，理论上是会丢失一些信息的。因为训练过程实际上还是数据驱动的，丢失掉一些信息让新 pose 处于训练集的空间里反而能更好地驱动人体。

Fig. 4: Ablation study of the pose projection strategy. (a,d) and (b,e) are the animation results without and with the pose projection strategy, respectively. (c,f) are the reference images with the closest pose in the training dataset.

Reference

[1]Animatable Gaussians: Learning Pose-dependent Gaussian Maps for High-fidelity Human Avatar Modeling