GoMAvatar-论文笔记

GoMAvatar: Efficient Animatable Human Modeling from Monocular Video Using Gaussians-on-Mesh

项目地址

CVPR 2024

Fig. 1: Overview

Abstract

本文介绍 GoMAvatar，这是一种实时、内存高效、高质量的可动画人体建模新方法。GoMAvatar 将单目视频作为输入，创建一个数字人，能够以新姿势重新建模，并从新的视角进行实时渲染，同时能够无缝集成基于光栅化的图形管道。本文方法的核心是网格高斯 (Gaussians-on-Mesh, GoM) 表示法，这是一种混合 3D 模型，结合了 3DGS 的渲染质量和速度，以及几何建模和可变形网格的兼容性。本文在 ZJU-MoCap、PeopleSnapshot 和各种 YouTube 视频上对 GoMAvatar 进行了评估。GoMAvatar 在渲染质量方面超过了当前的单目人体建模算法，在计算效率 (43 FPS) 方面明显优于这些算法，同时内存效率也很高 (每个主体 3.63 MB)。

Introduction

本文的主要创新点：

• 引入了网格高斯表示法，用于从单个视频中高效、高保真地重建人体，将 3DGS 与可变形网格相结合，实现实时、自由视点渲染。
• 为视角依赖性设计了一个独特的可微阴影模块，将颜色拆分为从 Gaussian splatting 得到的伪反照率图和从法线图得到的伪阴影图。

Method

Overview. 给定一个人的单目视频，目的是学习一个标准空间的 GoM 表示 $\text{GoM}_\theta^c$ (下标 $\theta$ 表示可学习的函数或变量，上标 $c$ 表示标准空间)，这样在给定相机内参 $K\in\R^{3\times3}$ 、相机外参 $E\in SE(3)$ 和人体 pose $P$ 时，就能渲染出对应的人体。为了渲染，首先将 $\text{GoM}_\theta^c$ 变换到观测空间：

$$\operatorname{GoM}^o=\text{Articulator}_\theta\left(\operatorname{GoM}_\theta^c, P\right) \tag{1}$$

• $\text{GoM}^o$ 表示观测空间的 GoM 表示

为了渲染出 $H\times W$ 的结果，用一个神经渲染器来获得人体的 appearence 和 alpha mask：

$$(I,M)=\text{Renderer}_\theta(K,E,\text{GoM}^o) \tag{2}$$

• $I\in\R^{H\times W\times3}$​​ 表示人体的 appearence
• $M\in\R^{H\times W\times1}$ 表示 alpha mask

最终的渲染结果是基于 $I$ 和 $M$ 通过经典的 alpha 合成得到的。

Gaussians-on-Mesh Representation

标准空间的 GoM 表示是通过点和面的集合以及相关属性来确定的：

$$\operatorname{GoM}_\theta^c \triangleq\left\{\left\{v_{\theta, i}^c\right\}_{i=1}^V,\left\{f_{\theta, j}\right\}_{j=1}^F\right\} \tag{3}$$

• $\{v_{\theta, i}^c\}_{i=1}^V$ 和 $\{f_{\theta, j}\}_{j=1}^F$ 分别表示 $V$ 个顶点和 $F$ 个面及其相关属性

可以进一步定义顶点为：

$$v^c_{\theta,i}=(p^c_{\theta,i},w_i) \tag{4}$$

• $p^c_{\theta,i}\in\R^3$ 表示顶点坐标
• $w_i\in\R^J$ 表示顶点和 $J$​ 个 joint 的混合蒙皮权重

定义面为：

$$f_{\theta,j}=(r_{\theta,j},s_{\theta,j},c_{\theta,j},\{\Delta_{j,k}\}_{k=1}^3) \tag{5}$$

• $r_{\theta,j}\in so(3)$ 和 $s_{\theta,j}\in\R^3$ 分别表示与面相关的局部高斯的旋转和缩放
• $c_{\theta,j}$ 表示颜色向量
• $\{\Delta_{j,k}\}_{k=1}^3$ 表示第 $j$ 个面所对应的 $3$ 个顶点的坐标，$\Delta_{j,k}\in\{1,...,V\}$​

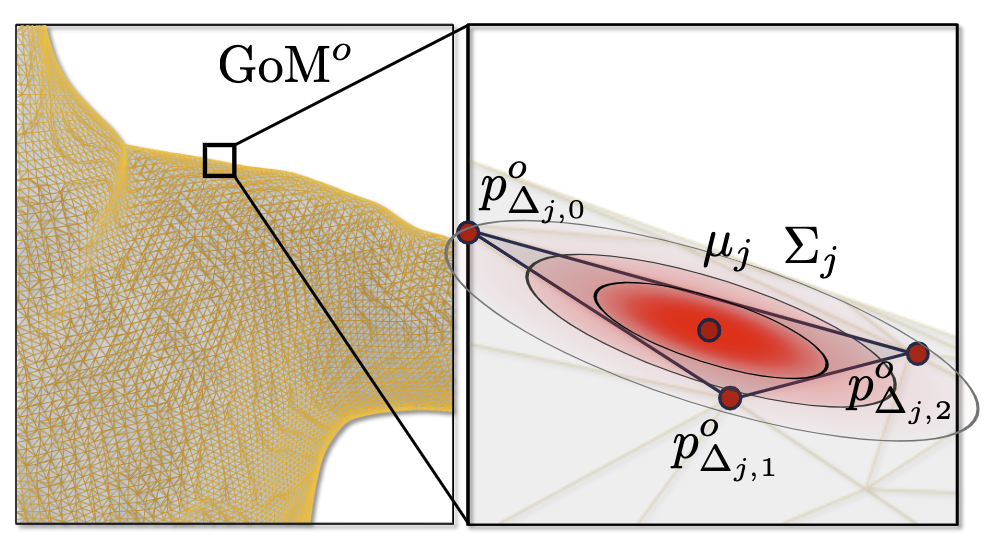Fig. 2: Gaussians-on-Mesh (GoM)

本文将高斯参数与面进行关联。如图 2 所示，在每个三角形的局部坐标系中学习高斯分布，并根据三角形的形状将它们转换到世界坐标系。将旋转矩阵 $r_{\theta,j}$ 初始化为0，将缩放因子 $s_{\theta,j}$ 初始化为1，从而使得初始时高斯分布在三角形的法线轴方向上是细长的。同时，椭球体 $\{x : (x−μ_j)^T Σ^{-1}_j (x−μ_j) = 1\}$ 在三角形上的投影是斯坦纳椭圆。

斯坦纳椭圆（Steiner ellipse），也称为内切椭圆，是一个在三角形内部的椭圆。它具有以下几个显著特征：

• 斯坦纳椭圆与三角形的每条边相切，且切点是三条边的中点；
• 它的中心位于三角形的重心（即三条中线的交点）。
• 在所有与三角形的三边相切的椭圆中，斯坦纳椭圆的面积最大；

Rendering

本文将最终的 RGB 图像 $I$ 拆分成伪反照率图 $I_{GS}$ 和伪阴影图 $S$：

$$I=I_{GS}\cdot S \tag{6}$$

• $I_{GS}$ 是由 Gaussian splatting 渲染出来的
• $S$​​ 是通过 mesh 光栅化后得到法线图预测出来的

Fig. 3: Pseudo shading map

伪阴影图如图 3 所示，这里我的理解就是 3DGS 渲染出来的图像 (伪反照率图) 再给他加上一层学出来的伪阴影图，伪阴影图是用来满足视角依赖性，不同视角预测不同的伪阴影图。

Pseudo albedo map $I_{GS}$ rendering. 通过给定世界坐标系下 $F$ 个高斯基元 $\{G_j\triangleq\mathcal{N}(\mu_j,\Sigma_j)\}_{j=1}^F$ 和对应的颜色 $\{c_{\theta,j}\}_{j=1}^F$，渲染出 $I_{GS}$ 和公式 2 中提到的 alpha mask $M$。

本文是在每个三角形面的局部坐标系中获取这些高斯参数，随后将这些局部高斯转换到世界坐标系中，并将各个面的变形考虑在内。这种独特的表述方式能够动态地适应三角形的不同形状，而这些三角形的形状在不同的人体姿势中会发生变化。具体来说给定一个公式 5 中的面 $f_{\theta,j}$，高斯基元在世界坐标系下的均值 $\mu_j$ 是这个三角形面的重心：

$$\mu_j=\frac{1}{3}\sum_{k=1}^3p^o_{\Delta_{j,k}} \tag{7}$$

• $p^o_{\Delta_{j,k}}$ 表示三角形面的三个顶点的坐标

高斯基元的协方差为：

$$\Sigma_j=A_j\left(R_j S_j S_j^T R_j^T\right) A_j^T \tag{8}$$

• $R_j$、$S_j$ 和 $A_j$ 分别是旋转、缩放和平移矩阵

通过公式 7 和 8 可以高斯基元可以自适应不同 pose 下的三角形形状。

Pseudo shading map $S$ prediction. 通过 mesh 光栅化法线图 $N_{mesh}$​ 来预测伪阴影图：

$$S=\text{Shading}_\theta(\gamma(N_{mesh})) \tag{9}$$

• $S\in\R^{H\times W\times1}$
• $\gamma(\cdot)$​ 表示和 NeRF 相同的 positional encoding
• $\text{Shading}_\theta$ 是个 $1\times1$ 的卷积神经网络

Articulation

在 LBS 将顶点从标准空间变换到观测空间之前，会用一个非刚体变换模块对标准空间的点进行一个位移，本文将这个非刚体变换称为“非刚体变换标准空间 (the non-rigidly transformed canonical space)”。

Linear blend skinning. LBS 已经很熟悉了，就直接跳过。

Non-rigid deformation. 在 LBS 之前会根据 pose 对每个顶点预测一个位移并加到顶点上：

$$p_i^{nr}=p_{\theta,i}^c+\text{NRDeformer}_\theta(\gamma(p_{\theta,i}^c,P)) \tag{10}$$

• $\text{NRDeformer}_\theta$ 表示一个 MLP

Pose Refinement

本文参考 Human-NeRF 加了一个 pose refinement 模块来对从视频里估计出来的 pose 进行改进。给定从视频中估计出来的人体的 pose $\hat{P}=\{(\hat{R}_j^p,t_j^p)\}_{j=1}^J$，预测一个正确的 joint 的旋转：

$$\left\{\xi_j\right\}_{j=1}^J=\operatorname{PoseRefiner}_\theta\left(\left\{\hat{R}_j^p\right\}_{j=1}^J\right) \tag{11}$$

• $\xi_j\in SO(3)$ 表示每个 joint 的旋转矩阵

最终的 pose $P=\left\{\left(R_j^p, t_j^p\right)\right\}_{j=1}^J=\left\{\left(\hat{R}_j^p \cdot \xi_j, t_j^p\right)\right\}_{j=1}^J$。pose refinement 只发生在新视图合成和训练阶段，以补偿视频中姿态估计的不准确性，动画时是不需要。

Training

本文渲染出来的 RGB 图像 $I$ 和 mask $M$ 进行监督，总体的 loss 为：

$$L=L_1+\lambda_{lpips}L_{lpips}+\lambda_ML_M+\lambda_{reg}L_{reg} \tag{12}$$

• $L_1$ 和 $L_M$ 分别是对 RGB 图像和 mask 求 L1 loss
• $L_{lpips}$ 是对 RGB 图像求 LPIPS loss

同时本文还对底层的 mesh 增加了一个正则项：

$$L_{reg}=L_{mask}+\lambda_{lap}L_{lap}+\lambda_{normal}L_{normal}+\lambda_{color}L_{color} \tag{13}$$

• $L_{mask}=||M_{mesh}-M_{gt}||$ 是对 mesh 的 mask 求 loss
• $L_{lap}=\frac{1}{N}\sum_{i=1}^N||\delta_i||^2$ 是拉普拉斯平滑 loss
• $L_{normal}$ 是最大化对相邻面的法向量的余弦相似度来保证法线的一致性
• $L_{color}$ 类似于 $L_{normal}$ 来使颜色保持平滑

本文首先通过 SMPL 来初始化顶点和面。为了丰富细节，对标准空间的 GoM 进行上采样，先在每条边的中心引入新的顶点，对底层 mesh 进行细分，然后用四个较小的面替换每个面实现上采样，新的面的属性会直接复制原始的面。

Reference

[1]GoMAvatar: Efficient Animatable Human Modeling from Monocular Video Using Gaussians-on-Mesh