SMPL-论文解析

SMPL: A Skinned Multi-Person Linear Model

项目地址

SIGGRAPH Asia 2015

Fig. 1: Overview

SMPL模型概述

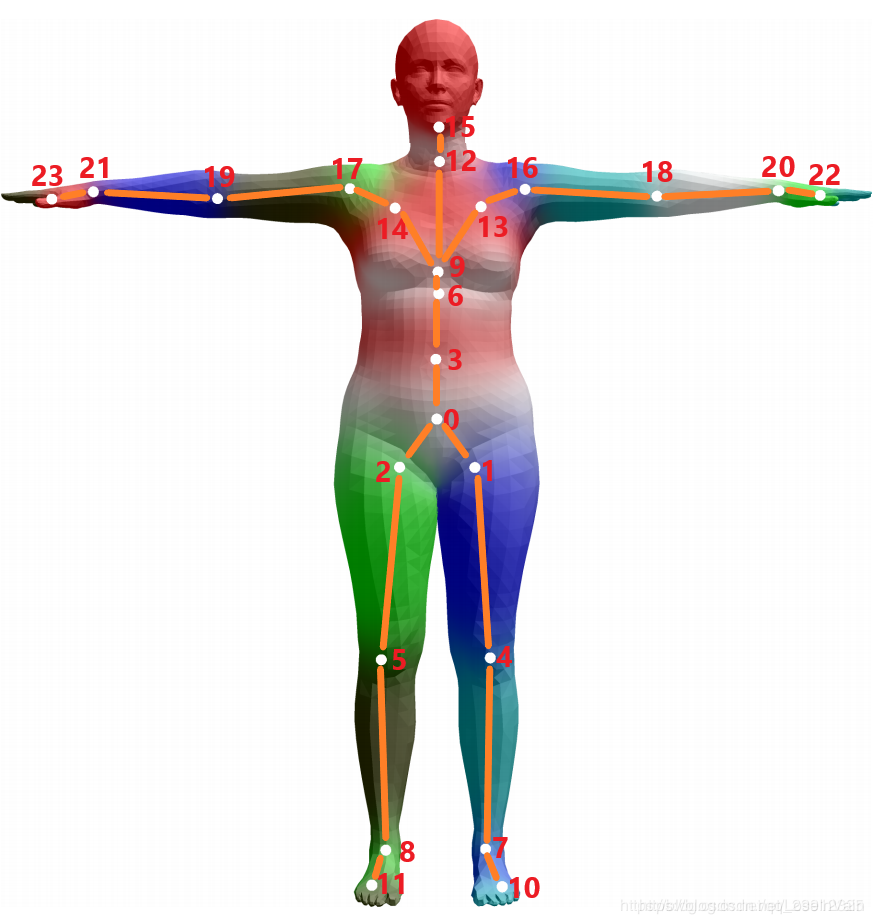
SMPL 是一种基于顶点的蒙皮模型，能准确表现自然人体姿势中的各种体形。简单来说就是可以表现各种姿态下不同体格 (高矮胖瘦) 的人。SMPL 分别用形状参数 (shape parameters) 来控制体格，用姿态参数 (pose parameters) 来控制不同的姿态，并且这些控制都是线性的。SMPL 模型包含 6890​ 个顶点和 24 个关节 (23 个关节点 + 1 个根节点)。

Fig. 2: SMPL模型的24个关节

SMPL中的参数

为了方便之后的讲解先把SMPL中的所有参数先列出来，具体含义之后会讲解：

$N$ 6890 个顶点

$K$ 23 个关节 (不包括根节点)

$\bar{\mathbf{T}}\in\R^{3N}$ 人体平均模型

$\mathcal{W}\in\R^{N\times K}$ 混合权重 (blend weights) 矩阵

$\vec\beta\in\R^{10}$ 体格参数 (shape parameters)，其实就是体格的 PCA 基

$\vec\theta\in\R^{72}$ 姿态参数 (pose parameters)，$23 \times 3 + 3 = 72$ (要加上根节点)，其实就是姿态的 PCA 基

$\vec\theta^*$​​ 标准姿态 (canonical pose \ rest pose \ T-pose \ zero pose) 下的姿态参数

$J(\vec\beta):\R^{\lvert\vec\beta\rvert}\mapsto\R^{3K}$​ 骨骼点位置估计函数 (joint location predict function)

$B_S(\vec\beta):\R^{\lvert\vec\beta\rvert}\mapsto\R^{3N}$ 基于体格的混合形状函数 (blend shape function)

$B_P(\vec\theta):\R^{\lvert\vec\theta\rvert}\mapsto\R^{3N}$​ 基于姿态的混合形状函数 (pose-dependent blend shape function)

$M(\vec\beta,\vec\theta;\bar{T},\mathcal{W},\mathcal{S},\mathcal{J},\mathcal{P}):\R^{\lvert\vec\theta\rvert\times\lvert\vec\beta\rvert}\mapsto\R^{3N}$ SMPL最终的一个方程，根据体格和姿态参数，映射到对应体格和姿态的顶点集。分号前的 2 个参数是人工指定的，分号后的 5 个参数是通过学习得到的，本文都采用这种格式。

• $\bar{\mathbf{T}}$ 人体平均模型
• $\mathcal{W}$​ 混合权重矩阵
• $\mathcal{S}$​ 体格的 PCA 系数矩阵
• $\mathcal{J}$ 骨骼点位置估计矩阵
• $\mathcal{P}$ 姿态的 PCA 系数矩阵

SMPL 模型最终就是要学习这 5 个参数。

Pipeline

SMPL 模型可以分为 4 个阶段：平均模版形状 (mean template shape)，基于体格的混合成形 (shape blend shapes)，基于姿态的混合成形 (pose blend shapesy) 和蒙皮 (skinning)；

平均模版形状 (Mean Template Shape)

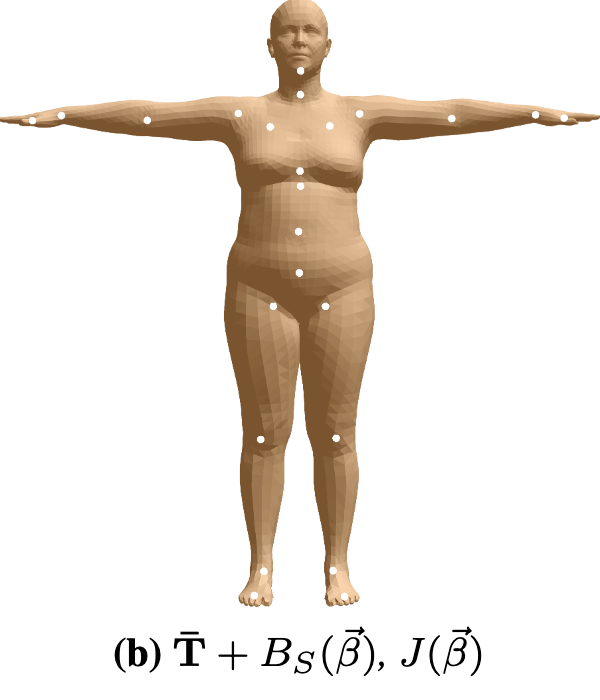
先定义一个在 T-pose 下的平均模板，可以认为它是一个基模板，后续基于体格和姿态的混合成形都是在这个集模板上进行参数的变化。这个模板是通过统计大量的真实人体 mesh，得到的均值形状，由 $N=6890$ 个顶点 (vertex) 和 13776 个面片 (mesh) 组成。

Fig. 3: 平均模板的 mesh，混合权重用颜色表示，关节用白点表示

基于体格的混合成形 (Shape Blend Shapes)

基于体格的混合成形就是在平均模板的基础上，加上基于体格的混合形状函数的偏移，形成新的 shape。这一步主要是用于改变人物的高矮胖瘦等体格特征，每个体格参数 $\beta$ 可以控制一项体格特征，具体的可视化可以参考SMPL模型Shape和Pose参数。

Fig. 4: 在平均模板上加上基于形状的偏移并且预测关节

基于姿态的混合成形 (Pose Blend Shapes)

不同的 pose 也会改变人物的 shape，比如弯腰的时候肚子上的肉会压缩，视觉上可能会显得变大。所以先把某一帧的 pose 导致的 shape 的改变加到 T-pose 下。

Fig. 5: 姿态对 T-pose 下的 shape 的影响

蒙皮 (Skinning)

最后通过线性混合蒙皮 LBS，将 T-pose 下的模型蒙皮到对应的 pose 下。

Fig. 6: 蒙皮后的模型

模型中的公式

首先要明确一点，无论是基于体格的混合成形还是基于姿态的混合成形，都是在求与平均模板的偏移 (offset)，求出来的偏移都是要加上平均模板上的顶点位置，才是最终的顶点位置。

基于体格的混合成形 (Shape Blend Shapes)

$$B_S(\vec\beta;\mathcal{S})=\sum_{n=1}^{\lvert\vec\beta\rvert}\beta_n\mathbf{S}_n \tag{1}$$

• $\vec\beta=[\beta_1,...,\beta_{10}]^T$

• $\lvert\vec\beta\rvert=10$ 表示体格参数的个数

• $\mathbf{S}_n\in\R^{3N}$​ 表示第 $n$ 个体格 PCA 基的系数

• $\mathcal{S}=[\mathbf{S}_1,...,\mathbf{S}_{10}]\in\R^{3N\times\lvert\vec\beta\rvert}$​ 表示体格的 PCA 系数矩阵

用公式 (1) 就能求出不同体格对于 shape 的偏移。

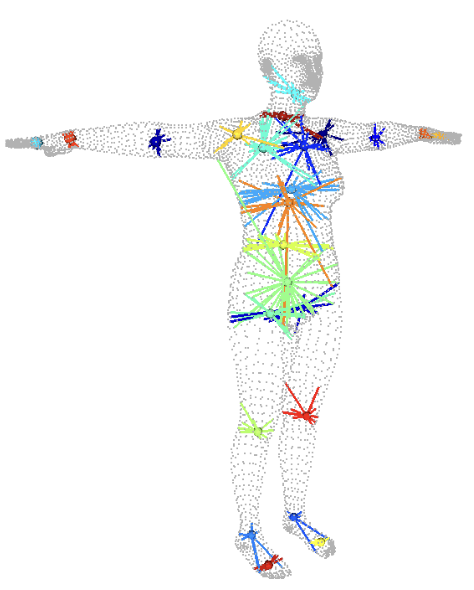
骨骼点位置估计

当经过基于体格的混合成形后，骨骼点的位置也会发生变换，不再是平均模板下的骨骼位置，因此需要对骨骼点进行位置估计，骨骼点的位置由它本身最为接近的若干个 mesh 的端点加权决定。

$$J(\vec\beta;\mathcal{J},\bar{\mathbf{T}},\mathcal{S})=\mathcal{J}(\bar{\mathbf{T}}+B_S(\vec\beta;\mathcal{S})) \tag{2}$$

• $\mathcal{J}\in\R^{3N\times 3K}$ 骨骼点位置估计矩阵

Fig. 7: 骨骼点位置估计的可视化

基于姿态的混合成形 (Pose Blend Shapes)

本文采用轴角 (Axis-angle) 表示旋转，$\vec\omega=(x,y,z)$ 表示以 $\bar{\omega}=\frac{\vec\omega}{\lVert\vec\omega\rVert}$ 为旋转轴，旋转 $\lVert\vec\omega\rVert$ 度。原文中姿态参数 $\vec\theta=[\vec\omega_0^T,...,\vec\omega_{23}^T]^T$ 表示关节 (0 号是根节点，1 ~ 23 是关节点) 关于其父节点的旋转，总共有 $3 \times 23 + 3 = 72$ 个参数。

$$\exp(\vec\omega_j)=\mathcal{I}+\hat{\bar{\omega}}_j\sin(\lVert\vec\omega_j\rVert)+\hat{\bar{\omega}}_j^2\cos(1-\lVert\vec\omega_j\rVert) \tag{3}$$

这个公式叫做 Rodrigues 公式，论文中是错的，原作者后面也进行了勘误。通过 Rodrigues 公式可以将轴角式转换成旋转矩阵，同时每个姿态参数也由原来的 3 个变成了旋转矩阵的 9 个。

$$B_P(\vec\theta;\mathcal{P})=\sum_{n=1}^{9K}(R_n(\vec\theta)-R_n(\vec\theta^*))\mathbf{P}_n \tag{4}$$

• $R(\vec\theta):\R^{\lvert\vec\theta\rvert}\mapsto\R^{9K}$ 表示将 pose 向量 $\vec\theta$ 映射为 Rodrigues 公式，参数个数变为 $23 \times 9 = 207$ 个
• $\mathbf{P}_n\in\R^{3N}$ 表示第 $n$ 个姿态 PCA 基的系数
• $\mathcal{P}=[\mathbf{P}_1,...,\mathbf{P}_{207}]\in\R^{3N\times 9K}$ 表示姿态的 PCA 系数矩阵

因为每个 pose 都是从 T-pose 变换过去的，如果想要保持线性，那就必须把 T-pose 下的旋转给减掉，这样才是相对于 T-pose 下的变换。

线性混合蒙皮LBS (Linear Blend Skinning)

$$\mathbf{t}'_i=\sum_{k=1}^Kw_{k,i}G'_k(\vec\theta,\mathbf{J})\mathbf{t}_i \tag{5}$$

• $\mathbf{t}_i$ 表示第 $i$ 个顶点蒙皮前的位置

• $\mathbf{t}'_i$ 表示第 $i$ 个顶点蒙皮后的位置

• $w_{k,i}$ 表示第 $k$ 个关节对第 $i$ 个顶点的蒙皮权重，是混合权重矩阵 $\mathcal{W}$ 中的一个元素

• $G'_k(\vec\theta,\mathbf{J})$ 表示从标准姿态到当前姿态的仿射变换矩阵。

对于 LBS 的更详细的介绍可以看这篇文章。

在经过 3.1、3.2 和 3.3 的之后，公式 (5) 可以进一步写为：

$$\mathbf{t}'_i=\sum_{k=1}^Kw_{k,i}G'_k(\vec\theta,J(\vec\beta;\mathcal{J},\bar{\mathbf{T}},\mathcal{S}))\mathbf{t}_{P,i}(\vec\beta,\vec\theta;\bar{\mathbf{T},\mathcal{S},\mathcal{P}}) \tag{6}$$

其中

$$\mathbf{t}_{P,i}(\vec\beta,\vec\theta;\bar{\mathbf{T},\mathcal{S},\mathcal{P}})=\bar{\mathbf{t}}_i+\sum_{m=1}^{\lvert\vec\beta\rvert}\beta_m\mathbf{s}_{m,i}+\sum_{n=1}^{9K}(R_n(\vec\theta)-R_n(\vec\theta^*))\mathbf{p}_{n,i} \tag{7}$$

• $\bar{\mathbf{t}}_i$ 表示平均模板上的第 $i$ 个顶点蒙皮前的位置

公式 (7) 就是对平均模板进行基于体格的混合成形和基于姿态的混合成形后的 shape，也就是加偏移的过程。

SMPL-X 预训练模型参数

SMPL-X 默认的是 1 个根节点 + 21 个身体 joints + 3 个头部 joints (1 个下巴 + 2 个眼睛) + 30 个手部 joints (15 个左手 + 15 个右手) + 21 个 extra joints + 51 个面部 landmarks = 127 个 joints，当然有些 projects 会选择 127 + 17 个面部轮廓 landmarks = 144 个 joints，不过可以控制的 joints 还是只有 1 + 21 + 3 + 30 = 55 个。

10 个 shape 参数 $\beta$，10 个 pose 参数 $\theta$，10 个 expression 参数 $\psi$。在 SMPL-X 中，N = 10475，K = 54 (不包括根节点)。

• v_template: [10475, 3] 存放的是每个顶点的坐标；

• vt: [11313, 2] vertex texture，存放的是顶点对应 UV 图中的坐标；

• f: [20908, 3] 存放的是每个面片由哪 3 个顶点组成，总共 20908 个面片；

• ft: [20908, 3] face texture，存放的是 vt 中三个点的 idx，表示每个面片在 UV 图中是由哪三个顶点组成；

• lmk_faces_idx: [51] 存放的是 FLAME 面部 landmarks 的面片；

• lmk_bary_coords: [51, 3] 存放的是 FLAME 面部 landmars 的重心坐标。重心坐标可以理解为就是 landmarks 的坐标，面部的 landmarks 总共有 51 个；

• dynamic_lmk_faces_idx: [79, 17] 存放的是脖子的旋转角度对应的 FLAME 脸部轮廓的面片；

• dynamic_lmk_bary_coords: [79, 17, 3] 存放的是脖子的旋转角度对应的 FLAME 脸部轮廓 landmarks 的重心坐标。脸部轮廓的 landmarks 总共有 17 个，脖子的可以旋转 79 度；

• J_regressor: [55, 10475] joint 回归器，总共有 55 个joint；

• kintree_table: [2, 55] 存放的是关节树表，即每个 joint 的父节点的 idx

• joint2num: 字典，存放的是每个 joint 的 idx，没啥用

• part2num: 字典，存放的是每个 part 的 idx，也没啥用

• weights: [10475, 55] 存放的是每个顶点与 joint 之间的权重

• shapedirs: [10475, 3, 400] 存放的是 shape 的 PCA 系数，虽然有 400 个 PCA 基，但是只取前 20 个 (10 个 shape + 10 个 expression)；

• posedirs: [10475, 3, 486] 存放的是 pose 的 PCA 系数，9 * 54 = 486，为什么是 486 可以看基于姿态的混合成形 (Pose Blend Shapes)；

下面手的部分没必要看，因为会集成在 SMPL-X 模型中，在调整 shape 和 pose 的时候也会把手一起调整。

• hands_componentsl: [45, 45] 存放的是左手 shape 的 PCA 系数；
• hand_componentsr: [45, 45] 存放的是右手 shape 的 PCA 系数；
• hands_meanl: [45,] 存放的是左手 mean shape 的 $\beta$ 值；
• hands_meanr: [45,] 存放的是右手 mean shape 的 $\beta$ 值；
• hands_coeffsl: [1554, 45] 存放的是左手 pose 的 PCA 系数；
• hands_coeffsr: [1554, 45] 存放的是右手 pose 的 PCA 系数

Reference

[1]SMPL: A Skinned Multi-Person Linear Model

[2]人体动作捕捉与SMPL模型 (mocap and SMPL model)

[3]三维人体动捕模型 SMPL：A Skinned Multi Person Linear Model

[4]基于SMPL的三维人体重建-SMPL模型的计算与构建（3）

[5]SMPL模型Shape和Pose参数

[6]SMPL模型学习

[7]SMPL: A Skinned Multi-Person Linear Model论文解读

[8]Expressive Body Capture: 3D Hands, Face, and Body from a Single Image