FITE-论文笔记

Learning Implicit Templates for Point-Based Clothed Human Modeling

项目地址

ECCV 2022

Fig. 1: Overview

Abstract

我们提出的 FITE (First-Implicit-Then-Explicit) 是一个先隐后显的框架，用于为穿着服装的数字人建模。我们的框架首先学习表示粗略服装拓扑结构的隐式表面模板，然后利用模板指导点集的生成，进一步捕捉与姿势相关的服装变形（如褶皱）。我们的管道结合了隐式和显式表示法的优点，即能够处理不同的拓扑结构，并能有效捕捉精细细节。我们还提出了扩散蒙皮技术，以方便模板训练，尤其是宽松服装的模板训练，以及通过基于投影的 pose 编码从 mesh 模板中提取 pose 信息，而无需预定义的 UV 贴图或连通性。

Introduction

本文的主要贡献：

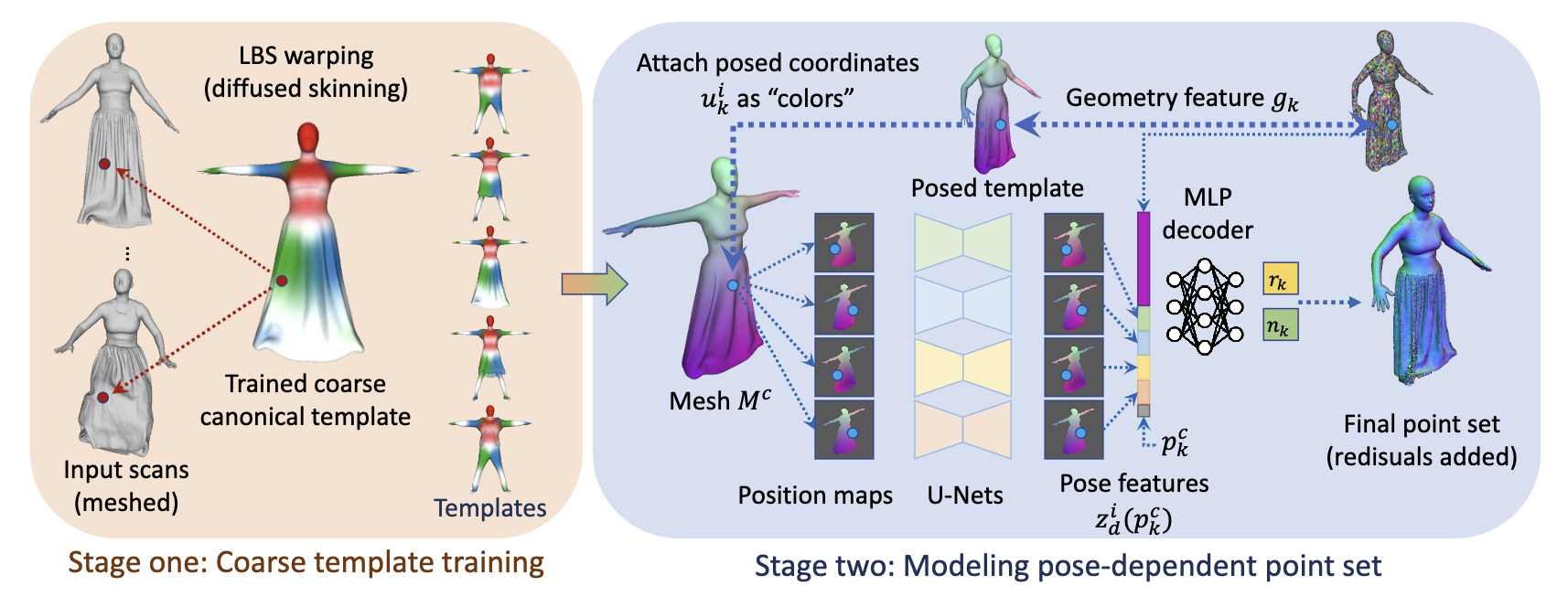
• 我们提出了一种先隐后显的穿衣人体建模框架，该框架融合了隐式和显式表示法的优点，与现有方法相比，具有更好的拓扑特性。
• 针对粗模板训练，我们提出了扩散蒙皮策略，即使在数据有限或服装宽松的情况下，也能预测出从标准空间到 pose 空间的稳定对应关系。
• 为了提取姿态信息，我们提出了基于投影的姿态编码，在没有预定义的 UV 贴图或连接性的前提下，可以通过训练后的模板学习出一个连续的特征空间。

Method

Fig. 2: Pipeline

Task Formulation and Notions

本文的任务是从一组不同服装、不同 pose 的输入中学习出逼真的可动画的穿衣数字人模型。图 2 是本文的 pipeline，第一阶段学习隐式模板，第二阶段预测依赖 pose 的位移。为了简化符号，先假设同一个人只穿一件衣服，后续会说明如何扩展到多件衣服。

本文假设输入是包含法线信息的点集形式，并且衣服覆盖了大部分的身体，因此可以从中提取出 GT 即占用场 (0 表示在外部，1 表示在内部)。对于第 i 帧输入的点集表示为 $\{p_k^i\}_{k=1}^{N_i}\subset \R^3$，其中 $N_i$ 表示第 i 帧输入点的数量，点 $p_k^i$ 处的法向量表示为 $n_k^i$。

LBS：

$$q^i=W(p,w(p),T,\theta^i)=\sum_{j=1}^{24}w_j(p)R^i_j(p) \tag{1}$$

• $p$ 和 $q^i$ 分别表示标准空间下一点的坐标和其对应第 i 帧 pose 所在位置的坐标
• $T$ 和 $\theta^i$ 分别表示 SMPL 在标准空间下的平均模板和第 i 帧的 pose 参数
• $w(p)=(w_1(p),\dots,w_{24}(p))\in\R^{24}$ 表示标准空间下的点 $p$ 对于每个 joint 的蒙皮权重，这个权重只是定义在 SMPL 的表面
• $R_j^i(p)$ 是由 $T$ 和 $\theta^i$​​ 确定的变换到第 i 帧 pose 的刚体变换矩阵

Stage One: Coarse Template Training with Diffused Skinning

本文用 0-1 占用场的 1/2 等值面 (1/2-level-set) 来表示服装的拓扑——也就是粗模板：

$$T^c=\{p\in\R^3:F^c(p)=1/2\} \tag{2}$$

• $T^c$ 表示粗模板
• $F^c(\cdot):\R^3\rarr[0,1]$ 表示 0-1 占用场

作者认为一个好的前向蒙皮权重场 $w_{\sigma_w}(\cdot):\R^3\rarr\R^{24}$ ($\sigma_w$ 是神经网络的参数) 应该具备以下两个特点：

1. 对于 SMPL 表面 $T$ 上的一点 $p$，$w(p)$ 应该和 SMPL 的蒙皮权重 $w^s(p)$ 相等；
2. $w$ 应该是从 SMPL 表面自然的 diffuse 出去的，即沿着 SMPL 的法线 $n^s(p)$ 方向的变化率应该是零；

这两个特点可以用以下公式来约束：

$$w(p)=w^s(p),\ \nabla_pw(p)\cdot n^s(p)=0,\ \ \mathrm{for} \ p\in T \tag{3}$$

因为蒙皮权重场 $w$ 沿着 SMPL 的法线 $n^s(p)$ 方向的变化率是零，所以 $w$ 的梯度 $\nabla_pw$ 与 SMPL 表面 $T$ 相切，又因为在 $T$ 上时 $w=w^s$，所以公式 3 等价于：

$$w(p)=w^s(p),\ \nabla_pw(p)=\nabla_Tw^s(p),\ \ \mathrm{for} \ p\in T \tag{4}$$

可以重新表述为最小化以下能量：

$$\lambda_p^s\int_{p\in T}||w(p)-w^s(p)||^2+\lambda_g^s\int_{p\in T}||\nabla_pw(p)-\nabla_Tw^s(p)||^2+\lambda_{reg}^s\int_{\R^3}||\nabla^2w||^2 \tag{5}$$

• $||\nabla^2w||^2$ 表示平滑正则化项

本文采用 PoissonRecon 来获取 $w$，$w$ 的每个 component 都是单独求解，并约束在 $[0,1]$ 范围内，最后重新进行归一化，整个过程如图 3 所示。

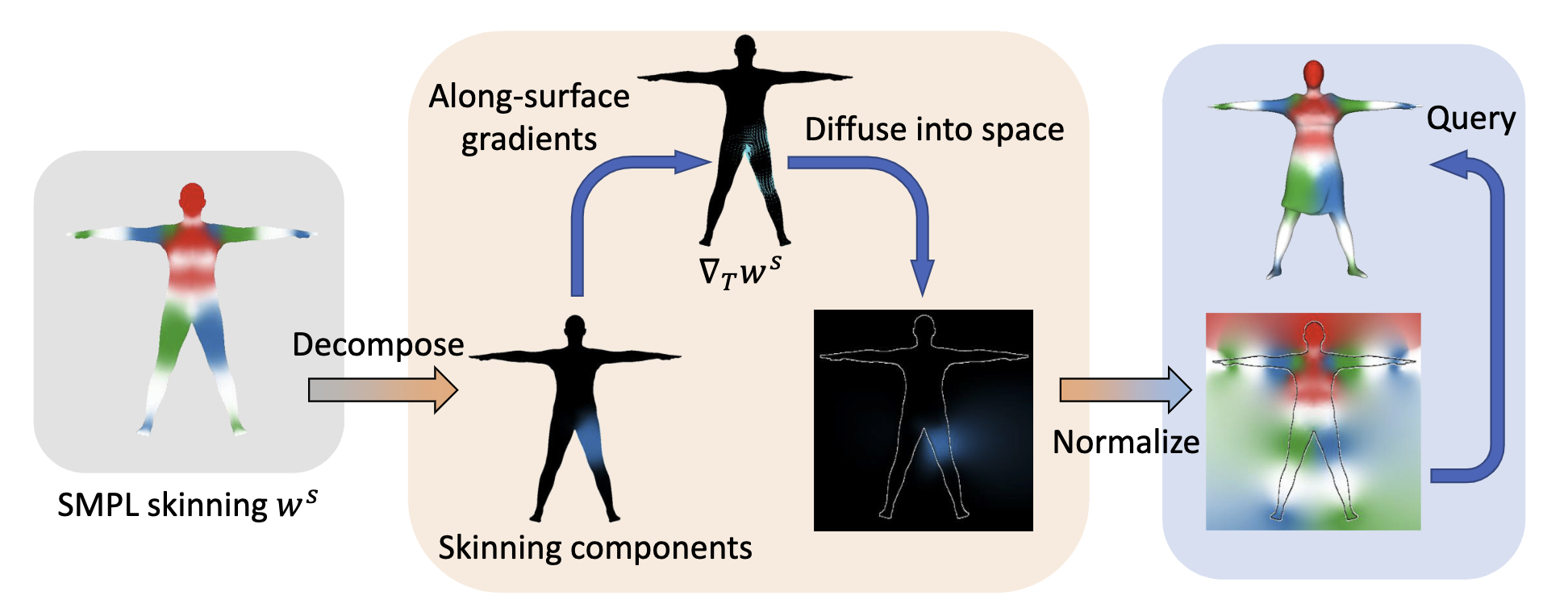
Fig. 3: Diffused skinning visualized. Each component of the skinning weights on SMPL is diffused independently and re-normalized to form a skinning field.

通过公式 5 的到 $w$ 后，就要训练和 pose 相关的标准空间占用场 $f_{\sigma_f}(\cdot,\theta^i):\R^3\to[0,1]$，第一阶段只要粗略的 shape 能用就停止，训练完成后把 $F^c$ 设置为：

$$F^c(p)=F_{\sigma_f}(p,\theta^{i_0}),\ \mathrm{where}\ \theta^{i_0}=\arg\min\{||\theta^i||_1:\theta^i\ \mathrm{in \ the\ training\ poses}\} \tag{6}$$

公式 6 其实就是从所有训练 pose 中挑选出 $L_1$ 范数下最接近 T-pose 的作为标准 shape。最后从 $F^c(p)$ 中提取 1/2-level-set $T^c$​ 作为标准模板。

Stage Two: Modeling Pose-Dependent Clothing Deformations

在得到标准空间的模板后，就可以通过 LBS 转换到 pose 空间：

$$q_k=W(p_k^c+c_k,w(p_k^c),T,\theta)+r_k \tag{7}$$

• $p_k^c$ 表示标准空间模板表面 $T^c$ 经过均匀采样后点集 $\{p_k^c\}_{k=1}^{N_c}$ 中的一个点
• $q_k$ 表示 $p_k^c$ 在 pose 空间中对应的那个点
• $c_k$ 和 $r_k$​ 分别是与 pose 无关的模板修正和与 pose 相关的变形，在本节后续会有更详细的说明

Pose-Agnostic Template Correction：由于 $T^c$ 只经过粗略训练，可能还缺乏某些细节，比如面部细节，而面部细节通常与 pose 无关。本文提出一种与 pose 无关的修正位移量 $c_k$ ，通过将几何特征 $g_k$ 输入 4 层的 MLP $C(\cdot)$ 来获得。

Projection-Based Pose Encoding：本文用图片来表示编码后的 pose 相关的特征，即 position maps。首先从模版表面提取 mesh，把 pose 空间点的坐标值加标准空间点的坐标值当作颜色，用正交投影的方式渲染成 position maps。和 Animatable Gaussians 获取 position maps 的过程类似，这里借用 Animatable Gaussians 中的图 (图 4) 来展示，只不过 Animatable Gaussians 是只用 pose 空间点的坐标值当作颜色。

Fig. 4: Position Maps in Animatable Gaussians

本文选取左前、左后、右前和右后四个角度，并且四个角度分别有略微覆盖头顶和脚底。最后用 U-Net encoders $U_d$ 来提取 pose 相关特征：

$$z_d^i=U_d(I_d^i)\in\R^{H\times W\times C_{pose}} \tag{8}$$

• $I_d^i\in\R^{H\times W\times 3}$ 表示第 i 个 pose 的 position maps
• $C_{pose}$ 表示 feature maps 的通道数
• $d=1,2,3,4$ 是四个角度的索引

Decoding Pose-Dependent Deformations：最后通过一个 8 层的 MLP $D(\cdot)$ 来生成公式 7 中的 $r_k$ 和基于投影的 pose 特征法线 $n_k$：

$$[r_k^c,n_k^c]=D([z^i(p_k^c),g_k]),\ \ \ r_k^c,n_k^c\in\R^3 \tag{9}$$

• $z^i(p)=[z_1^i(p),z_2^i(p),z_3^i(p),z_4^i(p)]$​
• $g_k$ 表示几何特征

当输入数据中有多套服装时，不同服装的模板在第一阶段分别训练，但共享 template corrector $C$、pose encoders $U_d$ 和 deformation decoder $D$​。

Training Losses

先跳过。

Reference

[1]Learning Implicit Templates for Point-Based Clothed Human Modeling