Gaussian Garments-论文笔记

Gaussian Garments: Reconstructing Simulation-Ready Clothing with Photorealistic Appearance from Multi-View Video

项目地址

arXiv

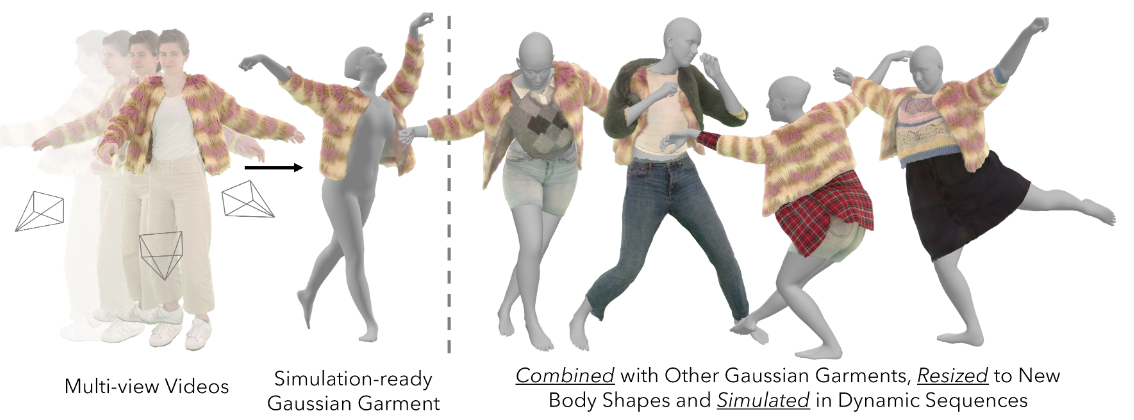Fig. 1: Overview

Abstract

我们介绍了高斯服装，这是一种从多视角视频中重建逼真的可模拟服装资产的新方法。我们的方法结合三维网格和高斯纹理来表示服装，高斯纹理同时编码了颜色和高频表面细节。这种表示方法可以从多视角视频中将服装几何图形准确地进行配准，并有助于将纹理的反照率 (固有颜色) 与光照效果区分开来。此外，我们还演示了如何对预先训练好的图神经网络（GNN）进行微调，以复制每件服装的真实行为。重建的高斯服装可自动组合成多件服装，并通过微调后的 GNN 制作动画。

Introduction

作者认为数字化衣服有三个关键点：衣服的 3D geometry、appearance 和 behavior/animation。本文用 3DGS 来表示这三点。

传统的多边形网格可以很好地表示服装的拓扑，但是很难通过可微优化直接从图片中获取网格。神经隐式表示可以对服装拓扑进行优化，但是很难对服装的动画进行仿真。因为 3DGS 是显式表示，因此可以对每个高斯基元进行单独地编辑，这样既可以优化拓扑也可以进仿真。

本文的核心是将基于网格的几何图形与基于高斯的外观建模相结合，主要贡献为：

• 利用 Gaussian splatting 技术重建真实世界服装的形状、外观和行为的综合管道
• 基于 Gaussian splatting 的优化程序，为多视角视频服装 mesh 进行配准的算法
• 是一种高斯服装表示方式，将三角形 mesh 与高斯纹理相结合，捕捉逼真的外观，可作为完全可控的 3D 资产使用。

Method

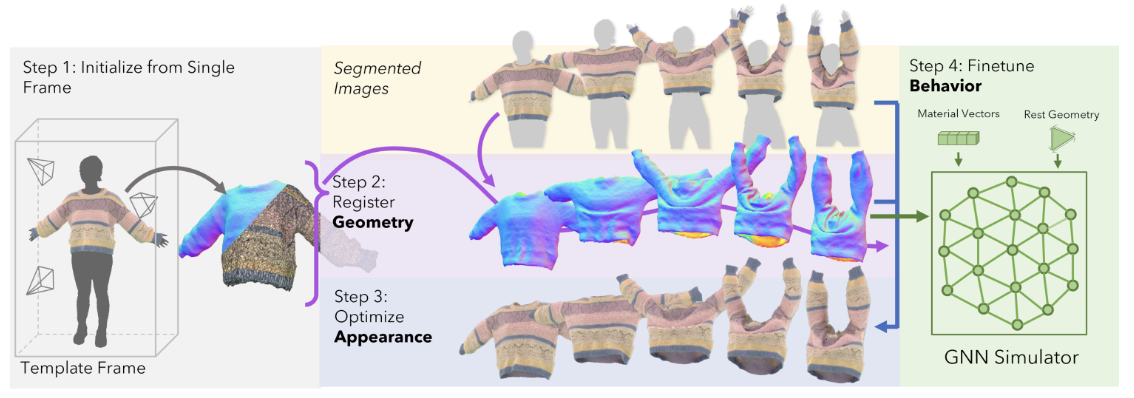Fig. 2: Pipeline

主要分为 4 步：

• 从多视角视频的一帧中初始化服装的几何和外观
• 对多视角视频中的衣服进行配准
• 通过视频序列对服装的外观进行优化
• 微调 GNN 网络来准确复现出服装的行为

Gaussian garment initialization

Mesh reconstruction

首先用 COLMAP 从模版帧中初始化点云；然后过滤掉背景点云并且用泊松表面重建算法重建出穿衣人体的表面；最后用语义分割图把衣服单独分割出来，用 re-meshing 算法获取衣服的 mesh。每件衣服的 mesh 都是 8000 个顶点。

Gaussian texture

Gaussian texture 对 3D mesh 表面和 2D 纹理图进行映射来控制表面的外观。纹理图上的每个点都定义了 3DGS 模型的一个参数：球谐函数系数 $\boldsymbol{\phi} \in [0,1]^{16\times3}$，不透明度 $\alpha$，缩放 $\mathbf{s}\in\R^3_+$，局部的旋转 $\mathbf{r} \in \mathbb{H}$ 和位移 $\boldsymbol{\mu} \in \R^3$，其中最后两项是在局部坐标系中。

首先在纹理图中进行采样，然后找到他在 mesh 中对应的面 $f_i$ 以及在 $f_i$ 中的重心坐标，这两个值定义了高斯基元在 mesh 表面的初始位置，本文把这个位置称为高斯的表面点 (surface point)。 这个表面点作为局部坐标系的原点，局部坐标系的基由 $f_i$ 的法向量以及表面上两个正交的向量组成 (见图 3 的左半边)。

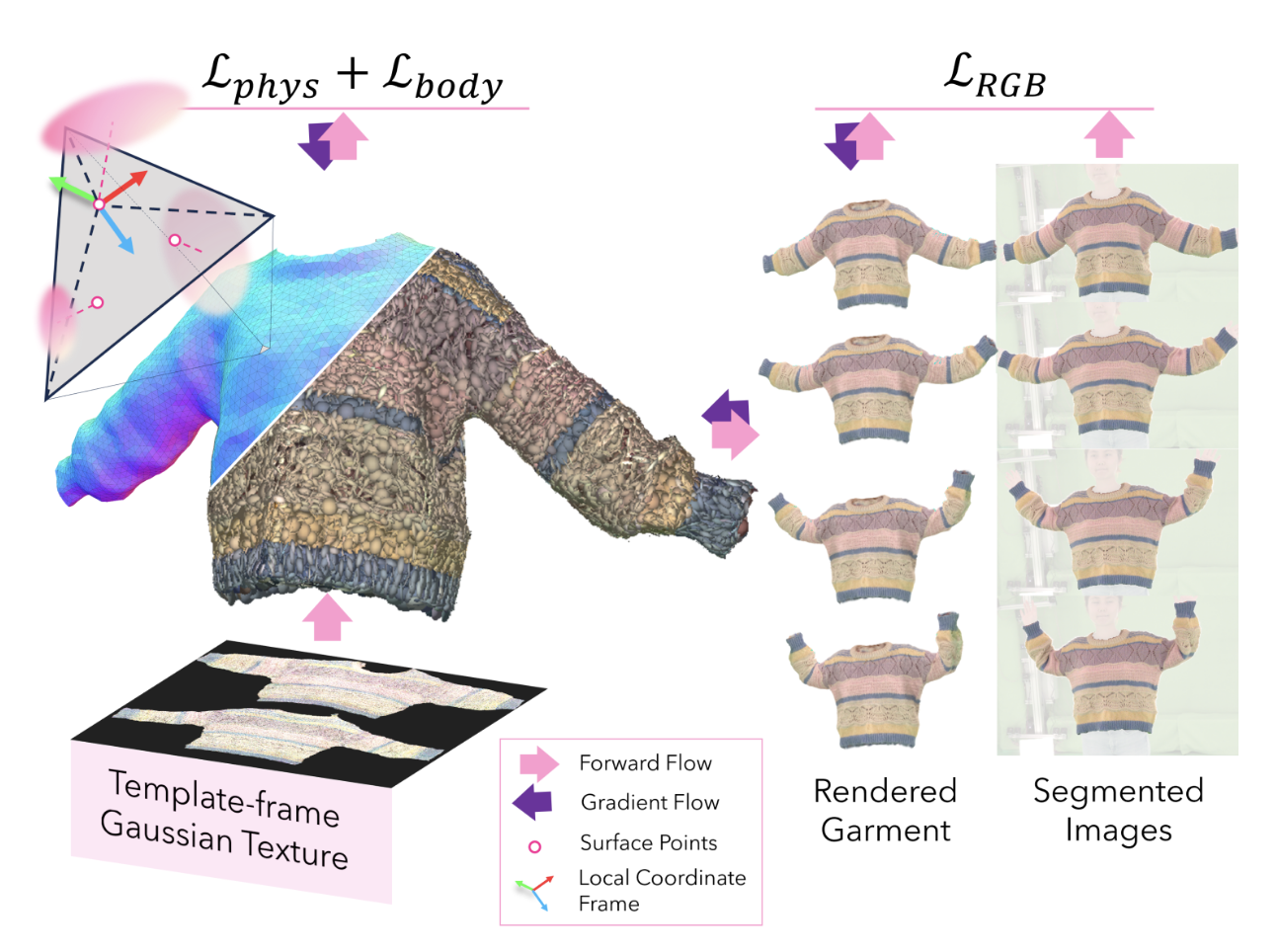Fig. 3: Register the garment mesh

Tracking-based registration

首先初始化外观，将高斯的参数都设置为 0，在 mesh 表面上创建高斯基元，通过优化参数来使衣服的外观与模版帧想匹配。主要通过 3 个损失函数来约束：

$$\mathcal{L}_{RGB}=\lambda_{RGB}\mathcal{L}_1+(1-\lambda_{RGB})\mathcal{L}_{SSIM} \tag{1}$$

$$\mathcal{L}_{pos}=||\max(\mu-\epsilon_{pos},0)||_2 \tag{2}$$

$\mathcal{L}_{pos}$ 用来约束高斯基元与表面点的距离，$\mu$ 表示局部位移，$\epsilon_{pose}$ 表示容许阈值。

$$\mathcal{L}_{scale}=||max(s-\epsilon_{scale},0)||_2 \tag{3}$$

$\mathcal{L}_{scale}$ 用来约束高斯基元的缩放，$s$ 表示缩放，$\epsilon_{scale}$ 表示容许阈值。

这样就能把 3D 高斯刚性固定在 mesh 的 face 上，这里得到的初始外观模型只用来进行 mesh 的配准，提高视觉质量会在下一节进行。在得到初始外观模型后需要对模版 mesh 进行配准，这一部分的关键是将梯度从图片空间传递到 mesh 上，本文通过技术渲染图片和 GT 之间的 $\mathcal{L}_{RGB}$ (和公式 1 一样) 来实现，把梯度从 3D 高斯传递到 mesh 上。

但是只用 RGB 来约束可能会导致 mesh 的扭曲 (图 4 Only-RGB 列)，因此本文还加入了很多物理能量的约束。

首先用弯曲能量 $\mathcal{L}_{bending}$ 来约束相邻 face 间的弯曲角度：

$$\mathcal{L}_{bending}=\sum_{(i, j)} \frac{\left\|e_{i j}\right\|^2}{a_{i j}} \operatorname{atan} 2\left(\sin \left(\theta_{i j}\right), \cos \left(\theta_{i j}\right)\right)^2 \tag{4}$$

• $(i,j)$ 表示相邻三角形的索引
• $\theta_{ij}$ 表示相邻三角形法向量之间的夹角
• $||e_{ij}||$ 表示两个三角形公共边的长度
• $a_{ij}$ 表示两个三角形的面积和

用应变能量 $\mathcal{L}_{strain}$ 约束三角形与模版帧中对应三角形的伸缩。这个应变能量是基于 St. Venant–Kirchhoff 材料模型，通过计算当前帧的几何 $x_t$ 与对应模版帧的几何 $X$ 之间的形变梯度 $\mathbf{F}=\frac{\partial x_t}{\partial X}$ 来约束：

$$\mathcal{L}_{strain}=\sum_i V_i\left(\frac{\lambda}{2} \operatorname{tr}\left(\mathbf{G}_i\right)^2+\mu \operatorname{tr}\left(\mathbf{G}_i^2\right)\right) \tag{5}$$

• $\mathbf{G}_i=\frac{1}{2}(\mathbf{F}_\mathbf{i}^T\mathbf{F}_\mathbf{i}-\mathbf{I})$ 表示面 $f_i$ 的 Green 应变张量
• $V_i$ 表示面的体积 (厚度乘上面积)
• $\lambda$ 和 $\mu$ 是 Lamé 参数，类似于权重

整体的物理正则项就是 $\mathcal{L}_{phys}=\mathcal{L}_{bending}+\mathcal{L}_{strain}$，但是只有物理正则项无法约束衣服和人体之间的关系，因此还需要用一个三次能量 (cubic energy) 来约束服装上的一个点与其最近的人体上的面之间的负法向距离：

$$\mathcal{L}_{body}=\sum_i \max \left(\epsilon_{body}-\left(\left(v_i-f_i\right) \cdot \vec{n}_i\right), 0\right)^3 \tag{6}$$

• $v_i$ 表示点的坐标
• $f_i$ 表示在人体的面上的点
• $\vec{n}_i$ 表示面的法向量
• $\epsilon_{body}$ 表示衣服与人体之间的安全阈值，本文设为 3mm

但是有些动作序列动作太大，导致两帧之间人体的动作差异巨大，这时候如果只是用 $\mathcal{L}_{body}$ 会导致衣服和人体之间发生穿透或者衣服的几何完全崩溃 (图 4 w/ body 列)。因此本文提出了虚拟边 (virtual edges) 正则项，沿着一个面的法线方向找到相交的另一个面，这两个对立面之间的连线就是虚拟边。对于所有这些对立的面，通过检查它们的法向量是否几乎平行来筛选出合适的面对，只会保留法线平行的面对和虚拟边。接着通过下面的损失函数 $\mathcal{L}_{VE}$ 来防止衣服网格自相交或坍塌：

$$\mathcal{L}_{VE}=\sum_i\max(L_{e_i}-l_{e_i},0)^2 \tag{7}$$

• $L_{e_i}$ 和 $l_{e_i}$ 分别是模版和当前帧的虚拟边 $e_i$ 的长度

$\mathcal{L}_{VE}$ 只会在优化的前半段替代 $\mathcal{L}_{body}$ ，后半段还是用 $\mathcal{L}_{body}$。

最后在配准过程中总的能量正则项为：

$$\mathcal{L}_{register}=\lambda_1\mathcal{L}_{RGB}+\lambda_2\mathcal{L}_{phys}+\lambda_3\mathcal{L}_{body} \tag{8}$$

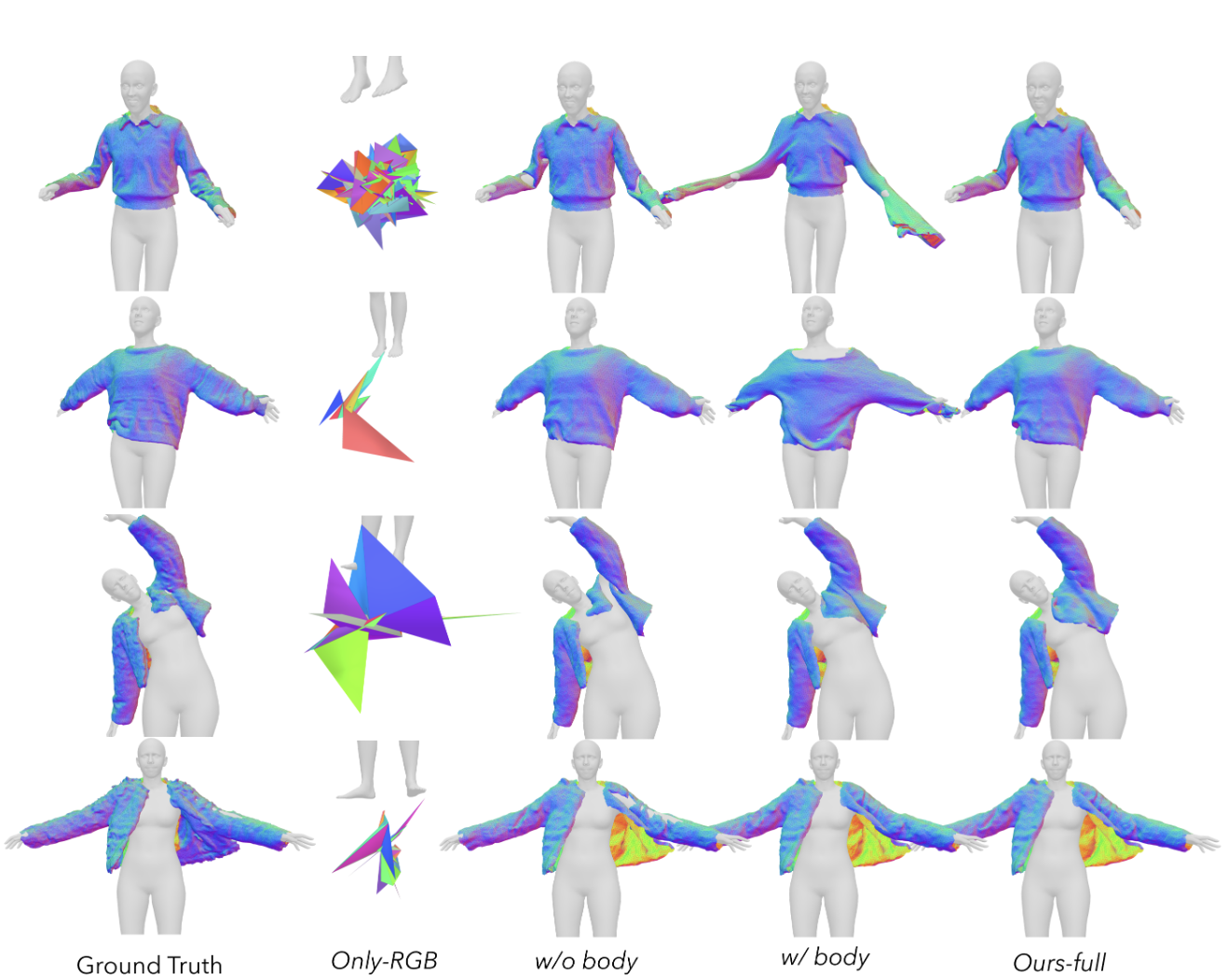Fig. 4: Ablation study of mesh registration

Appearance reconsturction

本文将服装的外观分成两个组成部份：

• 前文提到的高斯纹理 (Gaussian texture)
• 神经网络 $f_\theta$

本文的神经网络 $f_\theta$ 是 StyleUNet 用来提升纹理的质量，以 mesh 的反照率和遮挡贴图 $A$ 以及法向量图 $N$ 作为输入，输出的是纹理的球谐函数系数偏移 $\Delta\boldsymbol{\phi}$ 和位移偏移 $\Delta\boldsymbol{\mu}$ (这两个都是在原高斯纹理上的偏移量)。

球谐函数系数偏移可以将反照率和光照效果分开 (图 5)，位移偏移可以解释为观测噪声，目的是为了保留高频细节和表面的局部几何 (图 6)。

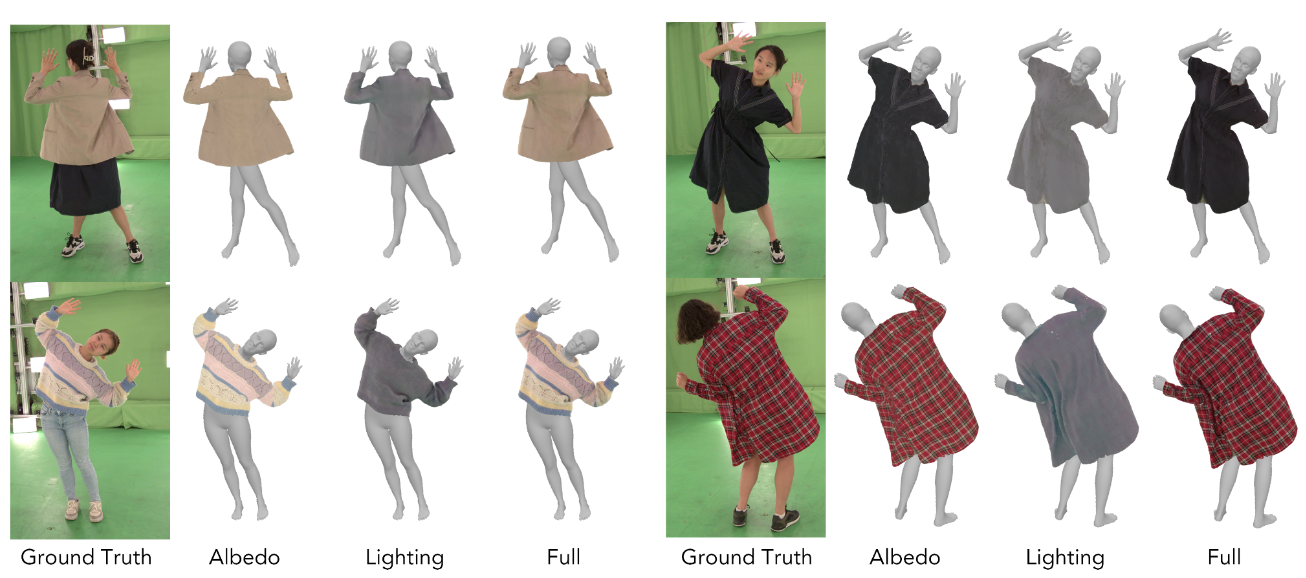Fig. 5: Disentangle the albedo color of the Gaussian Garments from the lighting effects

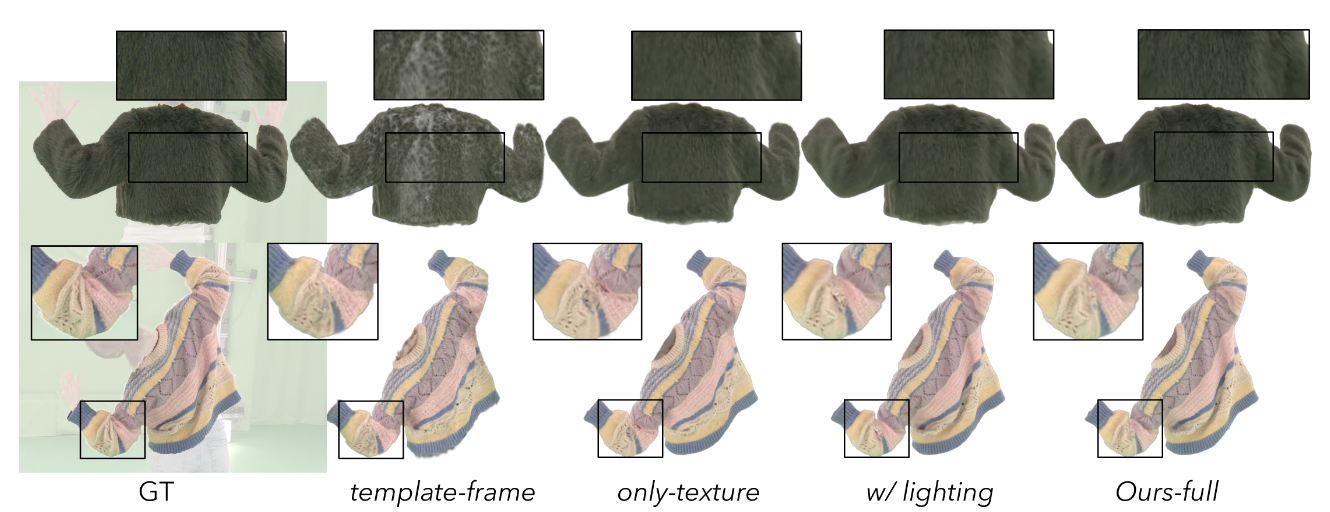Fig. 6: Ablations study of appearance model

最终高斯纹理 $\Omega$ 表示为：

$$\Omega=\{\boldsymbol{\phi}+\Delta \boldsymbol{\phi}, \alpha, \mathbf{s}, \mathbf{r}, \boldsymbol{\mu}+\Delta \boldsymbol{\mu}\} \in \mathbb{R}^{H \times W \times 59} \tag{9}$$

$$\Delta \boldsymbol{\phi},\Delta \boldsymbol{\mu}=f_\theta(A,N) \tag{10}$$

Mesh-based 3DGS rendering

对于多层衣服在进行 3DGS 渲染的时候，可能里面的衣服会有部份穿透到外面来 (如图 7A 所示)，为了解决这个问题，本文只渲染可见的表面点。因为每一件衣服都有一个对应的 mesh，本文就利用了 mesh 和高斯之间的耦合关系。对于每一个高斯基元，都会从相机投射出一条光线到对应的表面点，看这个表面点是否被其他 mesh 所遮挡，如果没有被遮挡才会渲染。

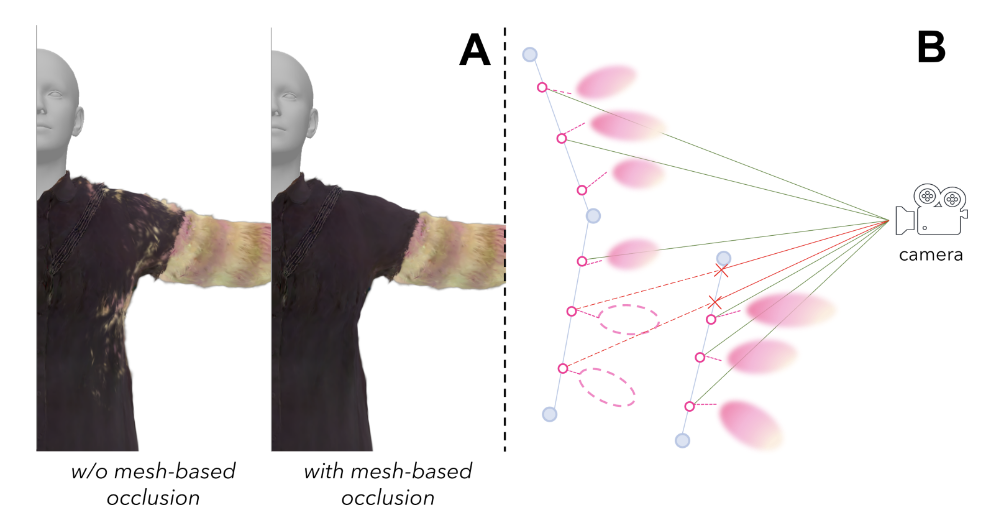Fig. 7

Behavior fine-tuning

本文用 ContourCraft 中的 GNN $g_{\psi}$ 来模拟衣服的动态，其中 $\psi$ 表示网络的参数，以 $t$ 帧的 mesh 节点的位置 $\mathbf{x}_t$、速度 $\mathbf{v}_t$、每个节点的材料向量 $\mathbf{m}$ 和每条边的静止几何 $\bar{E}$ 为输入，预测节点的关于下一帧的加速度 $\mathbf{\hat{a}}_{t+1}$：

$$\hat{\mathbf{a}}_{t+1}=g_\psi\left(\mathbf{x}_t, \mathbf{v}_t, \mathbf{m}, \bar{E}\right) \tag{11}$$

并且为了使服装的动态与真实观测到的衣服的动态更加拟合，本文还同时优化了模型的权重，材料向量和边的静止几何来最小化损失函数 $\mathcal{L}_{behavior}$。这个损失函数将预测的节点位置和配准的节点位置之间的均方误差与一组物理项结合：

$$\begin{aligned} \psi^*, \mathbf{m}^*, \bar{E}^* & =\underset{\psi^*, \mathbf{m}^*, \bar{E}^*}{\operatorname{argmin}}[ \left.\sum \mathcal{L}_{\text {behavior }}\left(g_\psi\left(\mathbf{x}_t, \mathbf{v}_t, \mathbf{m}, \bar{E}\right), \mathbf{a}_{t+1}\right)\right] \end{aligned} \tag{12}$$

• $\mathbf{a}_{t+1}$ 表示配准序列中第 $t+1$ 帧节点的加速度

Reference

[1]Gaussian Garments: Reconstructing Simulation-Ready Clothing with Photorealistic Appearance from Multi-View Video

[2]ContourCraft: Learning to Resolve Intersections in Neural Multi-Garment Simulations