REC-MV-论文笔记

REC-MV: REconstructing 3D Dynamic Cloth from Monocular Videos

项目地址

CVPR 2023

Fig. 1: Overview

Abstract

从单目视频中重建具有开放边界的动态 3D 服装表面是一个重要的问题，因为它为服装数字化提供了实用且低成本的解决方案。最近的神经渲染方法从单目视频中实现了高质量的动态服装人体重建结果，但这些方法无法将服装表面与身体分开。此外，尽管基于特征曲线表示的现有服装重建方法展示了从单个图像重建服装的令人印象深刻的结果，但它们很难为视频输入生成时间一致的表面。为了解决上述限制，在本文中，我们将此任务制定为 3D 服装特征曲线和单目视频表面重建的优化问题。我们引入了一种称为REC-MV 的新颖方法来联合优化服装的显式特征曲线和隐式符号距离场 (SDF)。然后可以通过规范空间中的服装模板注册来提取开放的服装网格。对多个随意捕获的数据集的实验表明，我们的方法优于现有方法，并且可以生成高质量的动态服装表面。

Introduction

目前有 2 种主流的解决方案，1) 利用神经渲染的方法，隐式表示标准空间下穿着衣服的人体，再用基于蒙皮的变形方法将其变形到对应的 pose。想要用这种方法使衣服与人体分离需要大量的工作。2) 直接从单目图像中重建高保真的衣物 mesh 模板，ReER 就使用特征曲线和隐式表面场的方法来重建衣物的模板。但是这些方法在以视频为输入时，很难保证重建出的衣服在时间上具有表面一致性。

本文结合神经渲染方法中的动态表面模型和显式特征曲线，使用基于蒙皮的运动建模来表示标准空间下的显示曲线和隐式表面，并通过从视频中自动提取的2D信息 (如图片像素，服装 mask 和可视化特征曲线) 来优化。主要贡献如下：

• REC-MV，第一个从单目视频中重建动态且拥有开放边界的宽松衣服的方法。
• 提出优化显式特征曲线和隐式服装表面的方法。
• 对于随意拍摄的单目视频，本文方法是SOTA。

Method

使用特征曲线 (领口、袖口、衣服下摆、裙摆等) 确定服装的轮廓，使用 SDF 来表示服装的表面。首先从视频中获取显式特征曲线和隐式服装表面，然后应用非刚性服装模板配准来提取开放边界服装 mesh。

Preprocessing：通过 Videoavatar 生成初始体格参数 (shape parameters) $\beta$，相机内参 $\pi$ 和每帧的 SMPL 姿态参数 (pose parameters) $\vec\theta$。使用 Self-Correction-Human-Parsing 的方法来估计服装 mask。还需要 2D 可见曲线 $\zeta=\{\zeta_{l,t}|l=1,...N_l,t=1,...,N_i\}$ (其中 $N_l$ 表示曲线的数量，$N_i$ 表示视频的帧数) 来恢复 3D 曲线，2D 可见曲线在分析服装 mask 的边界时会自动生成。

特征曲线和表面重建

显式表面模板 (Explicit Surface Template)：本文采用了几个表面模板 (包括上衣、连衣裙、外套、短裤和衬衫 )，模板包含预定义的 3D 特征曲线几何集 $\mathbf{L}=\{\mathbf{L}_i|i=1,...,N_l\}$ ($N_l$ 表示特征曲线的数量)，这些特征曲线是从服装的边界提取出来的。表面模板和预定义的特征曲线将分别用于服装表面和特征曲线的初始化。

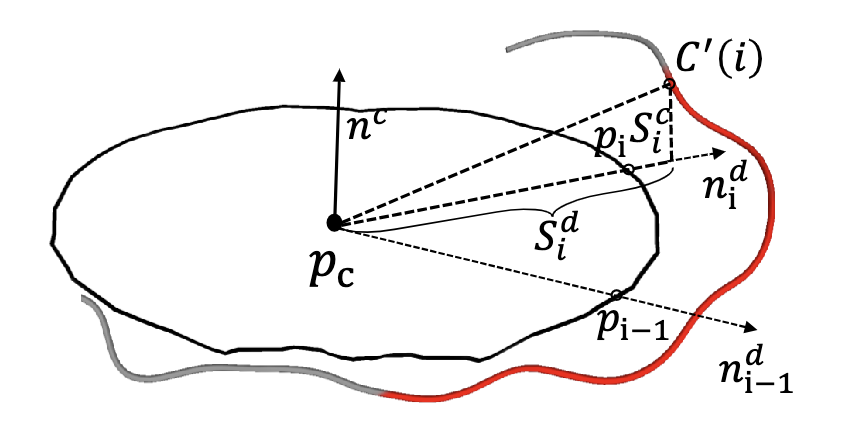
无交点曲线变形 (Intersection-free Curve Deformation)：如果直接将特征曲线表示为离散的点集，那么优化时对每个点进行 3D 变形偏移的时候，点的顺序可能会打乱，导致曲线交叉。所以本文提出了无交点曲线变形 (Intersection-free Curve Deformation) 的方法，点点变形由曲线中心和两个正交方向控制：

$$\mathcal{C}'(i)=\mathbf{p}_{\mathbf{c}}+S^d_i\mathbf{n}^{\mathbf{d}}_{\mathbf{i}}+S^c_i\mathbf{n}^{\mathbf{c}} \tag{1}$$

• $\mathcal{C}'(i)$​ 表示偏移后的点
• $\mathbf{p}_{\mathbf{c}}$ 表示曲线的中心
• $\mathbf{n}^{\mathbf{d}}_{\mathbf{i}}$ 表示曲线中心到当前点 $\mathcal{C}(i)$ 的方向
• $\mathbf{n}^{\mathbf{c}}=\frac{1}{N_p-1}\sum_{i=1}^{N_p}(\mathbf{n}^{\mathbf{d}}_{\mathbf{i}}\times\mathbf{n}^{\mathbf{d}}_{\mathbf{i-1}})$​ 表示垂直于特征曲线平面的方向
• $S^d_i\in\R,S^c_i\in\R$ 是可学习的参数，确定变形步长

Fig. 2: 可视化无交点曲线变形

标准空间的隐式 SDF (Implicit SDF in Canonical Space)：UDF 是可以表示开放表面的隐函数，但是在接近表面的点处不可微。因此本文用 SDF 来表示一个封闭的衣服表面，然后使用服装模板配准来提取开放表面的服装。本文并不使用一整个 SDF 来表示整个衣服表面，而是拆分成三种表面类型 (上衣、下衣和连体衣物 )，SDF 由具有可学习权重 $\eta$ 的 MLP $f$ 表示：$S(\eta)=\{\mathbf{p}\in\R^3|f(\mathbf{p};\eta)=0\}$

基于蒙皮的运动建模

对于大型身体运动，采用线性混合蒙皮 (LBS )，对于细粒度的变形则是采用非刚性变形场。

蒙皮转换 (Skinning Transformation)：用 SMPL 里的 LBS 方法进行蒙皮，但是蒙皮权重是仅针对 SMPL 表面上的点。为了将标准空间内的任意一点变换到相机空间，则需要用到扩散蒙皮策略 (diffused skinning strategy) 将 SMPL 顶点的蒙皮权重传播到整个标准空间，并将权重存储在 $256\times256\times256$ 的体素网格内，然后通过三线性插值获得蒙皮权重。

非刚性变形 (Non-rigid Deformation)：蒙皮使服装表面能够以与身体大规模运动一致的方式变形。然而，距离身体较远的部分服装的细节不能通过蒙皮完全表示。因此，要用非刚性变形 MLP 对这些细粒度变化进行建模。用 MLP $\mathcal{D}$ 来表示这个非刚性变形 ($\phi$ 是可学习的参数)：

$$\mathbf{p}'=\mathcal{D}(\mathbf{p},\mathbf{h},E(\mathbf{p});\phi) \tag{2}$$

• $\mathbf{p}$ 表示标准空间中的点
• $\mathbf{p}'$ 表示变换后的点
• $\mathbf{h}$ 表示当前帧的 latent code
• $E(\mathbf{p})$ 表示 NeRF 中的位置编码

最终结合蒙皮权重矩阵 $\mathcal{W}$，可以定义一个变形场 $\Phi(\cdot)=\mathcal{W}(\mathcal{D}(\cdot))$ 将标准空间内的任意一点变换到相机空间。

基于 2D 投影的 3D 特征曲线

初始化特征曲线 (Feature Curve Initialization)：使用服装模板提供的预定义的 3D 特征曲线几何集 $\mathbf{L}=\{\mathbf{L}_i|i=1,...,N_l\}$，本文直接最小化相机空间的 3D 特征曲线在的 2D 投影与 2D 可见曲线之间的倒角距离 (Chamfer Distance, CD)：

$$s,\mathbf{t},\mathbf{R}=\arg\min \mathrm{CD}(\Pi(\mathcal{W}(\bar{\mathbf{L}}_i)),\zeta) \tag{3}$$

$$\bar{\mathbf{L}}_i=s\mathbf{R}(\mathbf{L}_i)+t \tag{4}$$

• $\Pi$ 表示投影矩阵
• $\bar{\mathbf{L}}_i$ 表示变换后的特征曲线
• $\zeta$ 表示 2D 可见曲线
• $\mathbf{t}\in\R^3,\mathbf{R}\in SO(3),s\in\R$​ 分别表示优化后的平移、旋转和缩放参数

在经过刚性优化后，将 $\bar{\mathbf{L}}$ 设置为特征曲线集 $\{\mathcal{C}_i|i=1,...,N_l\}$ 的初始位置，用于之后的非刚性优化。

表面感知曲线的可见性估计 (Surface-aware Curve Visibility Estimation)：由于 2D 特征曲线 $\gamma$ 仅包含可见点，因此检测相机空间中 3D 曲线 $\mathcal{C}$ 上的点是否被人体遮挡至关重要。用等值面提取算法 (marching cube) 将标准空间的 SDF $S(\eta)$ 转换成显式的 mesh $\mathbf{T}_{\mathbf{s}}$，再通过变换场 $\Phi(\mathbf{T}_{\mathbf{s}})$ 将 mesh 从标准空间变换到相机空间，然后就可以基于 z-buffer 检测特征曲线上的点 $\Phi(\mathcal{C}(i))$ 是否被mesh 遮挡。

然而 3D 曲线 $\mathcal{C}$ 有时可能会移动到 mesh 的外部或者比 mesh 大，只依靠 z-buffer 检测可能会出现一些错误。因此本文还检测了相机空间中曲线上的点是否被 SMPL 身体上离其最近的点遮挡，能这么做是因为之前的无交点曲线变形几乎没有改变两者之间的关系。如果两项检测都通过，就被视为可见的。

曲线和表面协同优化

服装的表面由隐式 SDF 表示。由于特征曲线可见性估计取决于服装表面，因此曲线和表面在优化过程中必须保持一致性。为了确保优化过程中曲线可见性的准确性，我们联合优化曲线和和表面，同时进行正则化，使曲线位于 SDF 的零等值面上。通过基于可微表面渲染的光度损失最小化隐式表面。

曲线感知表面初始化 (Curve-aware Surface Initialization)：首先得到公式 (4) 中初始化后的特征曲线 $\bar{\mathbf{L}}$ ，然后用基于句柄的变形 (handle-based deformation) 方法使服装模板发生变形，使其特征曲线与 $\bar{\mathbf{L}}$ 对齐。最后使用隐式几何正则化 (Implicit Geometric Regularization, IGR) 的方法，通过拟合成变形后的服装模板来初始化隐式表面 $S(\eta)$。

可微表面渲染 (Differentiable Surface Rendering)：SelfRecon 里的方法，具体内容看 SelfRecon。

$$C_{\mathbf{p}}=f_c(\mathbf{p},\mathbf{n}_{\mathbf{p}}\mathbf{v}_{\mathbf{p}},\mathbf{z},E(\mathbf{p});\psi) \tag{5}$$

• $\mathbf{p}$ 表示表面上的交点
• $\mathbf{n}_{\mathbf{p}}=\nabla f(\mathbf{p};\eta)$ 表示交点的梯度
• $\mathbf{v}_{\mathbf{p}}$ 表示变换点 $\Phi(\mathbf{p})$ 的雅可比矩阵，用于将相机空间转换到标准空间
• $\mathbf{z}$ 表示视频帧的 latent code
• $f_c$ 表示颜色渲染网络
• $C_{\mathbf{p}}$ 表示点 $\mathbf{p}$ 的颜色

损失函数

显式特征曲线损失

特征曲线投影损失 (Feature Curve Projection Loss)：

$$\mathcal{L}_{proj}=\mathrm{CD}(V_{\mathcal{C}}\otimes\Pi(\Phi(\mathcal{C})),\zeta) \tag{6}$$

• $\mathcal{C}$ 表示 3D 特征曲线
• $\Phi(\cdot)$ 表示变形场，用于将点从标准空间变形到相机空间
• $\Pi$ 表示投影矩阵
• $V_{\mathcal{C}}$​ 表示曲线的可见性 mask
• $\otimes$ 表示 mask 选择操作
• $\zeta$ 表示 2D 可见曲线
• CD 表示倒角距离

特征曲线斜率正则化 (Feature Curve Slope Regularization)：为了保持 3D 曲线的曲率 (使整体曲线平滑且连续)，设置了斜率损失来保证相邻点之间的斜率一致性：

$$\mathcal{L}_{slop}=\sum_{i=1}^{N_p}(1-\cos<\mathbf{s_{i+1},\mathbf{s}_i}>) \tag{7}$$

• $\mathbf{s}_i=\mathcal{C}(i+1)-\mathcal{C}(i)$ 表示相邻两点组成的向量
• $N_p$ 表示曲线上点的数量
• $\cos<>$ 表示余弦相似度函数

表面正则化 (On-surface Regularization)：为了保证特征曲线在对应服装的表面，因此设定了尽可能接近 (as near as possible) 损失：

$$\mathcal{L}_{anap}=\sum_{i=1}^{N_p}|f(\mathcal{C}(i);\eta)| \tag{8}$$

• $f(\mathcal{C}(i);\eta))$ 是求曲线上一点 $\mathcal{C}(i)$​ 的 SDF 值

整体的显式特征曲线的损失如下：

$$\mathcal{L}_{curve}=\lambda_{proj}\mathcal{L}_{proj}+\lambda_{slop}\mathcal{L}_{slop}+\lambda_{anap}\mathcal{L}_{anap} \tag{9}$$

服装表面损失

对于 $N_i$ 帧的单目视频，可学习的隐式表面重建参数可以表示为 $\Theta=\{\eta,\phi,\psi\}\cup\{\mathbf{h}_i,\mathbf{z}_i|i=1,...,N_i\}$。

表面渲染损失 (Surface Rendering Loss)：我们用 SelfRecon 的方法渲染表面，先求出光线和标准空间表面的交点，然后用公式 (6) 的表面渲染网络预测颜色，其光度损失如下：

$$\mathcal{L}_{RGB}=\frac{1}{|\mathcal{R}|}\sum_{\mathbf{p}\in\mathcal{R}}|C_{\mathbf{p}}(\Theta)-I_{\mathbf{p}}| \tag{10}$$

• $\mathcal{R}$ 表示采样点集
• $I_{\mathbf{p}}$ 表示输入图像的像素值的 ground-truth

Mask 引导的隐式一致性损失 (Mask-guided Implicit Consistency Loss)：也是 SelfRecon 的方法，定期从标准空间的 SDF 中提取显示表面 mesh $\mathbf{T}_{\mathbf{s}}$，使用可微渲染器基于表面 mask 来迭代优化 mesh $\mathbf{T}_{\mathbf{s}}$，更新后的显示表面 $\hat{\mathbf{T}}_{\mathbf{s}}$ 将被用来监督 SDF $f$：

$$\mathcal{L}_{mcons}=\frac{1}{|\hat{\mathbf{T}}_{\mathbf{s}}|}\sum_{\mathbf{p}\in\hat{\mathbf{T}}_{\mathbf{s}}}|f(\mathbf{p};\eta)| \tag{11}$$

曲线引导的隐式一致性损失 (Curve-guided Implicit Consistency Loss)：通过 mask 损失来更新显示 mesh 可能导致衣服表面有洞或者发生塌陷，为了接近这个问题，设计了显式曲线和表面一致性损失。具体来说，对于属于两个服装的特征曲线 $\mathcal{C}$ (比如腰部曲线既属于上衣又属于下衣)，先生成闭合表面 $\mathbf{T}_\mathcal{C}$，然后从闭合表面 $\mathbf{T}_\mathcal{C}$ 采样 $N_a$ 个点来约束 SDF：

$$\mathcal{L}_{ccons}=\frac{1}{|\mathbf{T}_{\mathcal{C}}|}\sum_{\mathbf{p}\in\mathbf{T}_{\mathcal{C}}}|f(\mathbf{p};\eta)| \tag{12}$$

常见隐式损失 (Common Implicit Loss)：用了 Eikonal 损失 $\mathcal{L}_{eik}$ 来优化 SDF；为了避免非刚性变换的扭曲，使用刚性损失 $\mathcal{L}_{arap}$ 来约束非刚性变换；计算标准空间的法向损失 $\mathcal{L}_{norm}$ 来精细化表面；计算骨架平滑度损失以减少帧间 SMPL 姿态的高频抖动。总体隐式表面损失可以写为：

$$\mathcal{L}_{ims}=\mathcal{L}_{RGB}+\lambda_{mcons}\mathcal{L}_{mcons}+\lambda_{ccons}\mathcal{L}_{ccons}+\lambda_{arap}\mathcal{L}_{arap}+\lambda_{eik}\mathcal{L}_{eik}+\lambda_{norm}\mathcal{L}_{norm} \tag{13}$$

Reference

[1]REC-MV: REconstructing 3D Dynamic Cloth from Monocular Videos