NeRF-前置知识

体渲染 (Volume Rendering) 简介

体渲染技术主要是为了渲染云、烟、雾和火等非刚性物体，这些物体可以看作是一堆聚积在一起的粒子，当光线穿过这些物体时，光中的粒子光子 (Photons) 会与这些物体内部的粒子发生作用，可能被吸收或发生散射等现象，同时这些物体中的粒子本身也可能会发光，这些物体中的粒子被称为参与介质 (Participating Media)。体渲染技术最主流的是在医疗领域，比如 CT 和核磁共振等来获取人体内部的医学数据。

体数据

离散化后的体数据可以看成是由 体素 (Vixel) 组成的三维数组，vixel 这个单词是由 volume + pixel 组成，可以理解成是体中的像素，是体的最小单位，每个体素是一个正方体，其中存储的是颜色和密度等信息。

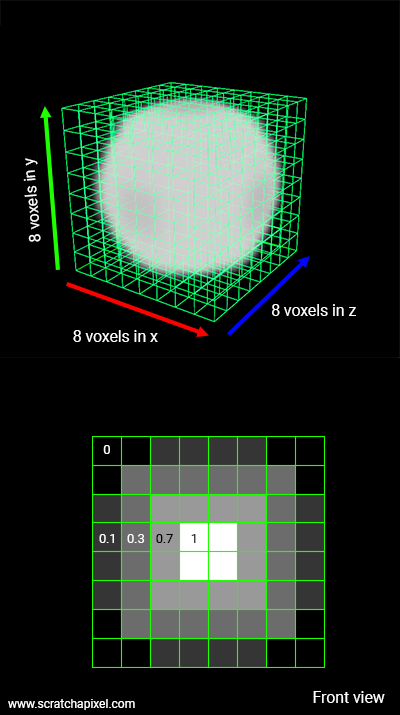Fig. 1：一个 8x8x8 的体素网格，每个体素内存储着密度的值

光线投射 (Ray Casting) 算法

每个像素对应一条光线，光线在经过体数据时进行采样，再利用后文提到的体渲染模型来求出每条光线的辐射强度。在体数据内进行采样的同时，会生成对应的强度剖面 (Intensity Profile)，图 3 中的 (c) 就是 NeRF 在体渲染过程中生成的强度剖面，横坐标表示采样点的位置，纵坐标表示该点的密度。

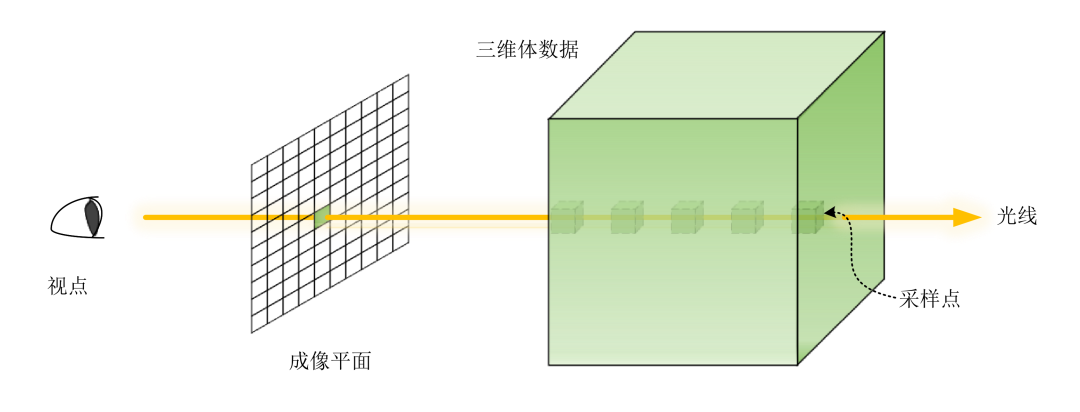Fig. 2：光线投射算法示意图

Fig. 3：NeRF 流程图

体渲染模型

当光线穿过参与介质时 ，光子会与其发生作用，我们假设一条光束只会与周围小部分区域内的参与介质发生作用，即图 4 粉色圆柱体内的粒子，且我们讨论的是此条光束 $L$ 的辐射强度，可以简化为以下 4 种模型 (当然真实世界远比这复杂)：

• 吸收 (Absorption)：光子被参与介质吸收，导致 $L$ 的辐射强度减少。
• 放射 (Emission)：参与介质本身也可能会发光，比如气体加热到一定的温度就会电离，电离子会获得能量，并以光子的形式释放出来。这些光子的运动方向是随机的，但最终会有一部分沿着光束的路径运动。因此放射会导致 $L$ 的辐射强度增加。
• 外散射 (Out-Scattering)：光子在撞击到参与介质后，可能会发生弹射，导致部分光子散射出 $L$，会减少 $L$ 的辐射强度。
• 内散射 (In-Scattering)：其他光束的光子在撞击后，可能会进入到 $L$，且方向和 $L$ 相同，这样就会增加 $L$ 的辐射强度

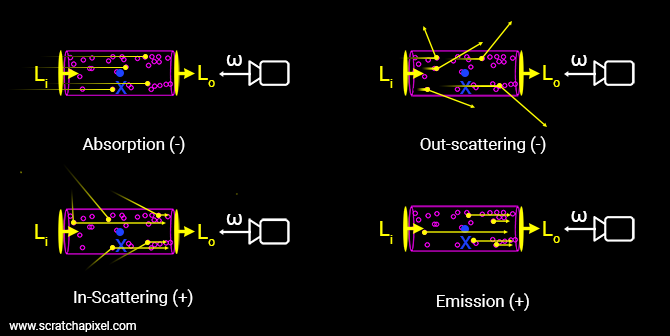Fig. 4

图 4 中 $L_i$ 和 $L_o$ 分别表示入射光和出射光，$\omega$ 表示的是视角方向即相机光线方向。

参考 Max 1995 年的论文 Models for Direct Volume Rendering，只考虑吸收和放射就可以对 NeRF 中的颜色积分方程进行推导。

吸收模型 (Absorption Only)

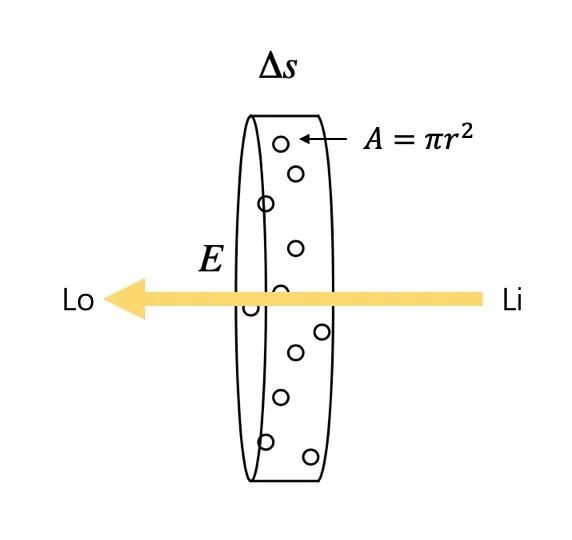Fig. 5

如图 5 所示，粒子的半径为 $r$，投影面积 $A=\pi r^2$，单位体积内粒子数为$\rho$，底面积为 $E$，宽度为 $\Delta S$，光沿着垂直于底面的方向传播，$L_i$ 表示入射光，$L_o$ 表示出射光。圆柱体体积为 $E\Delta s$，包含 $N=\rho E \Delta s$ 个粒子，假设 $\Delta s$足够小，且粒子没有重叠，那么这些粒子在底面上遮挡的总面积是 $NA=\rho AE\Delta s$。所以一束光通过这个圆柱体的时候，有 $\frac{\rho AE\Delta s}{E}=\rho A\Delta s$ 的概率会被遮挡，即出射光的辐射强度是入射光辐射强度的 $(1-\rho A\Delta s)$ 倍，数学上可以表示为：

$$\Delta I=-\rho(s)A\Delta sI(s) \tag{1}$$

其中 $s$ 是光进入 Volume (也可以称为物体空间 Object Space) 后的距离，$I(s)$ 是 $s$ 处的辐射强度。当 $\Delta s \to 0$ 时，就有如下的微分方程：

$$\frac{dI}{ds}=-\rho(s)AI(s)=-\tau(s)I(s) \tag{2}$$

$\tau(s)=\rho(s)A$ 称为消光系数(Extinction Coefficien)，定义了光子被遮挡的比例。该微分方程的解是：

$$I(s)=I_0\exp \begin{pmatrix} -\int_0^s\tau(t)dt \end{pmatrix} \tag{3}$$

其中 $I_0$ 是 $s=0$ 处的辐射强度，即光进入 Volume 的位置。可以定义

$$T(s)=\exp \begin{pmatrix} -\int_0^s\tau(t)dt \end{pmatrix} \tag{4}$$

为 0 到 $s$ 处的透明度 (Transparency ，在 NeRF 中称为透射率 Transmittance)。

在体渲染中，消光系数 $\tau$ 经常也被简称为不透明度 (Opacity)，但是对于边长为 $l$ 的体素，从平行于一条边的角度看过去，其不透明度 $\alpha$ 实际上是：

$$\alpha=1-T(l)=1-\exp \begin{pmatrix} -\int_0^l\tau(t)dt \end{pmatrix} \tag{5}$$

放射模型 (Emission Only)

假设图 1 中的参与介质是透明的 (即这些粒子不会吸收光)，单位投影面积的辐射强度为 $C$，由之前推导出来的投影面积 $\rho AE\Delta s$可知，这些粒子总共提供 $C\rho AE\Delta s$ 的光通量，则单位面积的平均光通量为 $\frac{C\rho AE\Delta s}{E}=C\rho A\Delta s$，同样可以得到微分方程：

$$\frac{dI}{ds}=C(s)\rho(s)A=C(s)\tau(s)=g(s) \tag{6}$$

其中 $g(s)$ 称为 源项 (Source Term)，表示 $s$ 处放射的辐射强度。这个微分方程的解如下：

$$I(s)=I_0+\int_0^sg(t)dt \tag{7}$$

和公式 3 中的指数不同，公式 7 中的积分是没有上限的，因为辐射强度可以随着宽度 $s$ 的增加不断累积。

吸收放射模型 (Absorption Plus Emission)

实际上，参与介质既会吸收光子导致入射光的辐射强度减少，同时自身又会发光增加辐射强度。所以结合前两个模型可以得到以下微分方程：

$$\frac{dI}{ds}=g(s)-\tau(s)I(s) \tag{8}$$

微分方程的解为：

$$I(D)=I_0\exp \begin{pmatrix} -\int_0^D\tau(t)dt \end{pmatrix} +\int_0^Dg(s)\exp \begin{pmatrix} -\int_s^D\tau(t)dt \end{pmatrix} ds \tag{9}$$

其中积分下限 0 表示 Volume 的边界位置，上限 D 表示眼睛的位置，第一项表示背景光的辐射强度乘上整个 Volume 的透明度，第二项是源项在每个位置 $s$ 提供的辐射强度乘上该位置 $s$ 到 眼睛 $D$ 的透明度 $T'(s)=\exp\begin{pmatrix}-\int_s^D\tau(t)dt\end{pmatrix}$，因此最后整理为：

$$I(D)=I_0T(D)+\int_0^Dg(s)T'(s)ds \tag{10}$$

微分方程求解过程

对于公式 8，将 $\tau(s)I(s)$ 移到等式左边，两边同乘积分因子 $\exp\begin{pmatrix}\int_0^s\tau(t)dt\end{pmatrix}$ 得到：

$$\begin{pmatrix} \frac{dI}{ds}+\tau(s)I(s) \end{pmatrix} \exp \begin{pmatrix} \int_0^s\tau(t)dt \end{pmatrix}=g(s)\exp \begin{pmatrix} \int_0^s\tau(t)dt \end{pmatrix} \tag{A}$$

等式左边是两个乘积的微分：

$$\frac{d}{ds}(I(s)\exp\begin{pmatrix} \int_0^s\tau(t)dt \end{pmatrix})=g(s)\exp \begin{pmatrix} \int_0^s\tau(t)dt \end{pmatrix} \tag{B}$$

对等式两边同时从 $s=0$ 到 $s=D$ 进行积分得到：

$$I(D)\exp \begin{pmatrix} \int_0^D\tau(t)dt \end{pmatrix}-I_0=\int_0^D\begin{pmatrix} g(s)\exp \begin{pmatrix} \int_0^s\tau(t)dt \end{pmatrix} \end{pmatrix}ds \tag{C}$$

将 $I_0$ 移到等式右侧，并且两边同乘 $\exp\begin{pmatrix}-\int_0^D\tau(t)dt\end{pmatrix}$ 就可以得到公式 9。

NeRF 中的体渲染

积分颜色方程

将公式 10 与 NeRF 最后的颜色积分方程 $C(\textbf{r})$ ：

$$C(\textbf{r})=\int_{t_n}^{t_f}T(t)\sigma(\textbf{r}(t))\textbf{c}(\textbf{r}(t),\textbf{d})dt, \ where\ T(t)=\exp \begin{pmatrix}-\int_{t_n}^t\sigma(\textbf{r}(s))ds \end{pmatrix} \tag{11}$$

对比可以发现：

• NeRF 少了第一项 $I_0T(D)$，即忽略了背景光的影响
• NeRF 中的体积密度 $\sigma(\textbf{r}(t))$ 表示参与介质在 $\textbf{r}(t)$ 处的密度，$\textbf{c}(\textbf{r}(t),\textbf{d})$ 表示在视角 $\textbf{d}$ 下 $\textbf{r}(t)$ 处的颜色即辐射强度 (在 NeRF 中辐射强度可以理解为颜色)，因此公式 11 中的 $\sigma(\textbf{r}(t))\textbf{c}(\textbf{r}(t),\textbf{d})$ 表示的是 $\textbf{r}(t)$ 处放射的辐射强度和公式 10 中的源项 $g(s)$ 是等价的。
• Max 的论文认为光是从 Volume 的边界位置传播到眼睛，而 NeRF 认为是从近平面传播到远平面，方向刚好相反，因此公式 11 中的 $T(t)$ 的上下限和公式 10 中的 $T'(s)$ 的上下限刚好相反。如图 6 所示，$s$ 到 $D$ 和 $t_n$ 到 $t$ 其实表示的是同一段光线。

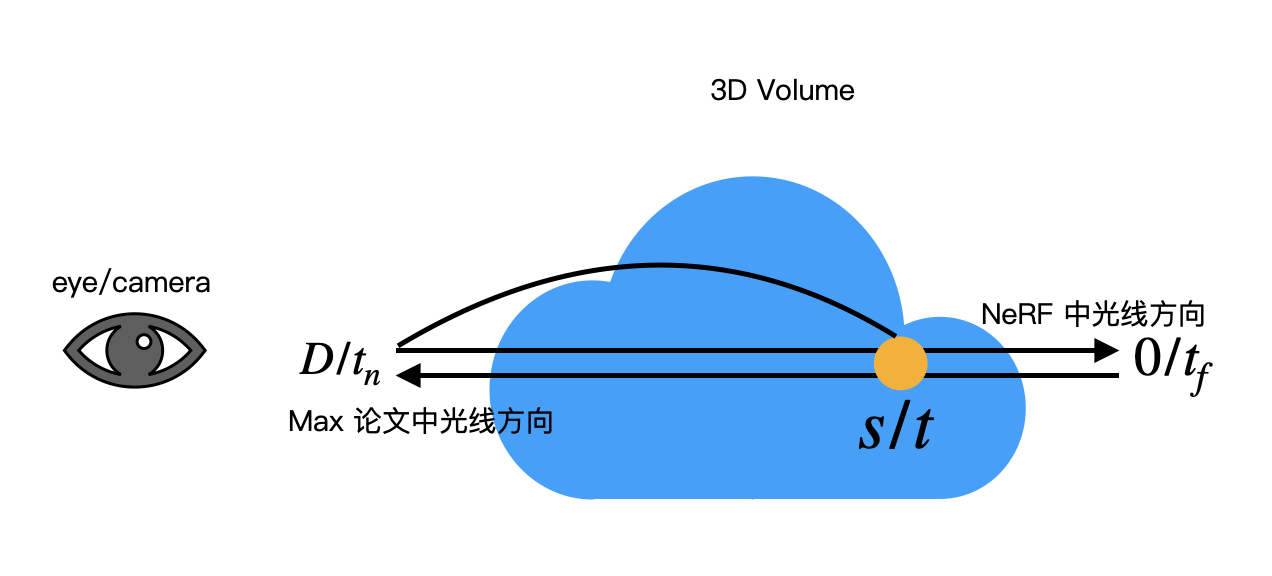Fig. 6

离散颜色方程

公式 11 在计算机中是无法表示的，只能通过离散化，采样光线上的点来近似计算积分，根据 Max 的论文可知最简单的近似计算积分的方法是黎曼和 (Riemann Sum)，将整条光线划分为 N 个等距的区间 ，每个区间的长度为 $\delta_i =\frac{t_f-t_n}{N}=t_{i+1}-t_i$，我们假设每个区间内的密度 $\sigma$ 和颜色 $\textbf{c}$ 是处处相等且为 $\sigma_i$ 和 $\textbf{c}_i$，因此区间 $[t_i,t_{i+1}]$ 的颜色可以近似为 ：

$$\begin{align} \nonumber\hat{C}(t_i\to t_{i+1})&=\int_{t_i}^{t_{i+1}}T(t)\sigma_i\textbf{c}_idt \\ &=\sigma_i\textbf{c}_i\int_{t_i}^{t_{i+1}}T(t)dt \tag{12} \end{align}$$

其中 $T(t)=\exp\begin{pmatrix}-\int_{t_n}^t\sigma_ids\end{pmatrix}$ 可以进一步拆分为两个区间的积分：

$$\begin{align} \nonumber T(t)&=\exp\begin{pmatrix}-\int_{t_n}^t\sigma_ids\end{pmatrix}\\ \nonumber&=\exp\begin{pmatrix}-(\int_{t_n}^{t_i}\sigma_ids+\int_{t_i}^t\sigma_ids)\end{pmatrix}\\ \nonumber&=\exp\begin{pmatrix}-\int_{t_n}^{t_i}\sigma_ids\end{pmatrix}\exp\begin{pmatrix}-\int_{t_i}^t\sigma_ids\end{pmatrix}\\ &=T_i\exp\begin{pmatrix}-\int_{t_i}^t\sigma_ids\end{pmatrix} \tag{13} \end{align}$$

所以公式 12 就变为：

$$\begin{align} \nonumber\hat{C}(t_i\to t_{i+1})&=\sigma_i\textbf{c}_i\int_{t_i}^{t_i}T_i\exp\begin{pmatrix}-\int_{t_i}^t\sigma_ids\end{pmatrix}dt\\ \nonumber&=\sigma_i\textbf{c}_iT_i\int_{t_i}^{t_{i+1}}\exp\begin{pmatrix}-\sigma_i(t-t_i)\end{pmatrix}dt\\ \nonumber&=\sigma_i\textbf{c}_iT_i\frac{\exp\begin{pmatrix}-\sigma_i(t-t_i)\end{pmatrix}}{-\sigma_i}\bigg|_{t_i}^{t_{i+1}}\\ \nonumber&=T_i(1-\exp\begin{pmatrix}-\sigma_i(t_{i+1}-t_i\end{pmatrix})\textbf{c}_i\\ &=T_i(1-\exp\begin{pmatrix}-\sigma_i\delta_i\end{pmatrix})\textbf{c}_i \tag{14} \end{align}$$

公式 14 中的 $1-\exp\begin{pmatrix}-\sigma_i\delta_i\end{pmatrix}$ 可以简化为第 $i$ 个区间的不透明度 $\alpha_i$，最后将每一区间的颜色累加起来就可以近似表示整条光线的颜色：

$$\begin{align} \nonumber\hat{C}(\textbf{r})&=\sum_{i=1}^NT_i(1-\exp\begin{pmatrix}-\sigma_i\delta_i\end{pmatrix})\textbf{c}_i\\ &=\sum_{i=1}^NT_i\alpha_i\textbf{c}_i \tag{15} \end{align}$$

根据之前提到的黎曼和的方法，可以将 $T_i$ 也离散化：

$$\begin{align} \nonumber T_i &= \exp\begin{pmatrix}-\int_{t_n}^{t_i}\sigma_ids\end{pmatrix}\\ &\approx \exp(-\sum_{j=1}^{i-1}\sigma_j\delta_j) \tag{16} \end{align}$$

显而易见 $T_i$ 表示的是从近平面 $t_n$ 到第 $i$ 个采样点 $t_i$ 所累积的透射率，最后结合公式 15 和 公式 16 就可以得到 NeRF 论文中的公式 3。

采样

逆变换采样 (Inverse Transform Sampling)

在讲逆变换采样之前，先了解几个概念。

概率密度函数 (Probability Density Function, PDF) 是一个描述随机变量在某个确定的取值点附近的可能性的函数，横坐标为随机变量的取值，纵坐标是该取值的概率密度，注意纵坐标并不是概率，随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。连续型随机变量的概率密度函数是 PDF，离散型随机变量在各特定取值上的概率称为概率质量函数 (Probability Mass Function, PMF)。

累积分布函数 (Cumulative Distribution Function, CDF) 又称为分布函数，累积分布函数的定义为 $F_X(x)=P(X\le x)$，即对 PDF 进行 $-\infin$ 到 $x$ 的积分或对 PMF 累加到 $x$，无论连续性随机变量还是离散型随机变量都有 CDF。

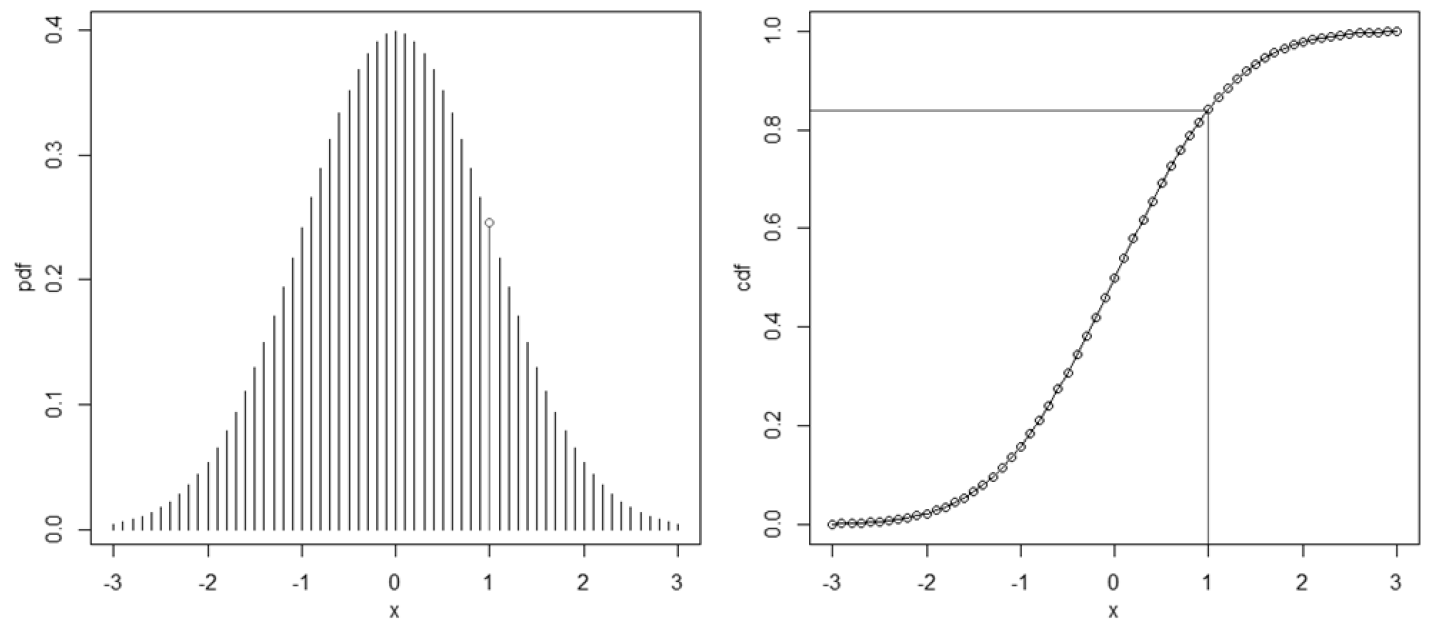Fig. 7：正态分布的 PDF（左）和 CDF（右）

逆变换采样主要是为了解决蒙特卡罗 (Monte Carlo) 方法中如何基于概率密度函数进行采样这一难题。要使用逆变换采样，前提是要知道累积分布函数 $F(x)$，然后求出 CDF 的逆函数 $G(y)=F^{-1}(x)$，很明显 CDF 的值域是 $[0,1]$，因此其逆函数的定义域是 $y\in[0,1]$。最后在 $G(y)$ 的定义域内进行均匀采样，每个点的函数值就是符合概率密度函数的采样点。

NeRF 中的分层采样 (Hierarchical Sampling)

分层采样策略是 NeRF 中一个很重要的 trick，采样率越高最后的结果肯定也越好，但是计算机的资源有限，我们不可能无限提高采样率。所以可以用分层采样，在不提高采样率的前提下，尽可能的在密度高的地方进行采样。

因为物体中参与介质的密度并不是均匀的，有些地方的密度很高，有些地方的密度趋近于零，因此如果对整条光线只是采取均匀采样的策略，那么可能会在一些参与介质密度很低的地方进行太多次采样，导致采样效率过低。分层采样将进行 2 次采样，分别为粗 (Coarse) 采样和细 (Fine) 采样。

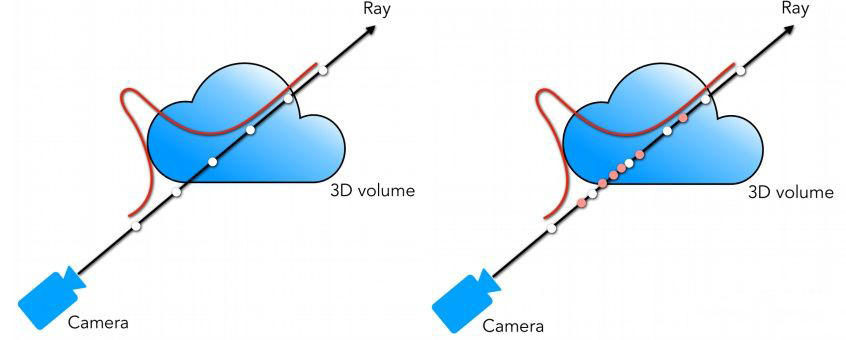Fig. 8：粗采样（左）和细采样（右）

粗采样是在光线上均匀采样 64 个点，采样集通过公式 15 可以初步算出颜色 $\hat{C}_c(\textbf{r})=\sum_{i=1}^{N_c}T_i\alpha_i\textbf{c}_i$，进一步把 $T_i\alpha_i$ 整合成一个权重 $w_i$ 就可以得到：

$$\hat{C}_c(\textbf{r})=\sum_{i=1}^{N_c}w_i\textbf{c}_i \tag{17}$$

$\alpha_i$ 表示第 $i$ 个区间的不透明度，不透明度越大表示这个区间内的参与介质密度越高；$T_i$ 表示的是从近平面 $t_n$ 到第 $i$ 个采样点 $t_i$ 所累积的透射率，透射率越大光线从 $t_n$ 传播到 $t_i$ 过程中没有碰撞到其他参与介质的概率就越高。因此把这两项的乘积当作权重 $w_i$，当 $w_i$ 越大时，该区间的辐射强度就越大，越值得被采样。将权重归一化为 $\hat{w}_i=w_i/\sum_{j=1}^{N_c}w_j$，得到的就是概率密度函数 (PDF)。细采样根据得到的 PDF 使用逆变换采样 (Inverse Transform Sampling) 采样 128 个点，将粗采样的 64 个点和细采样的 128 个点作为采样集最后算出 $\hat{C}_f(\textbf{r})$。(图 8 粗采样和细采样的示意图中，白色的点是粗采样的点，橙色的点是细采样的点，红色的曲线就是 PDF)

NeRF 中的逆变换采样通俗地来说就是把 PDF 即 $\hat{w}_i$ 给累加起来转换成 CDF，在 CDF 的纵坐标上进行均匀采样 128 个点，每个点的横坐标就是细采样的采样点。

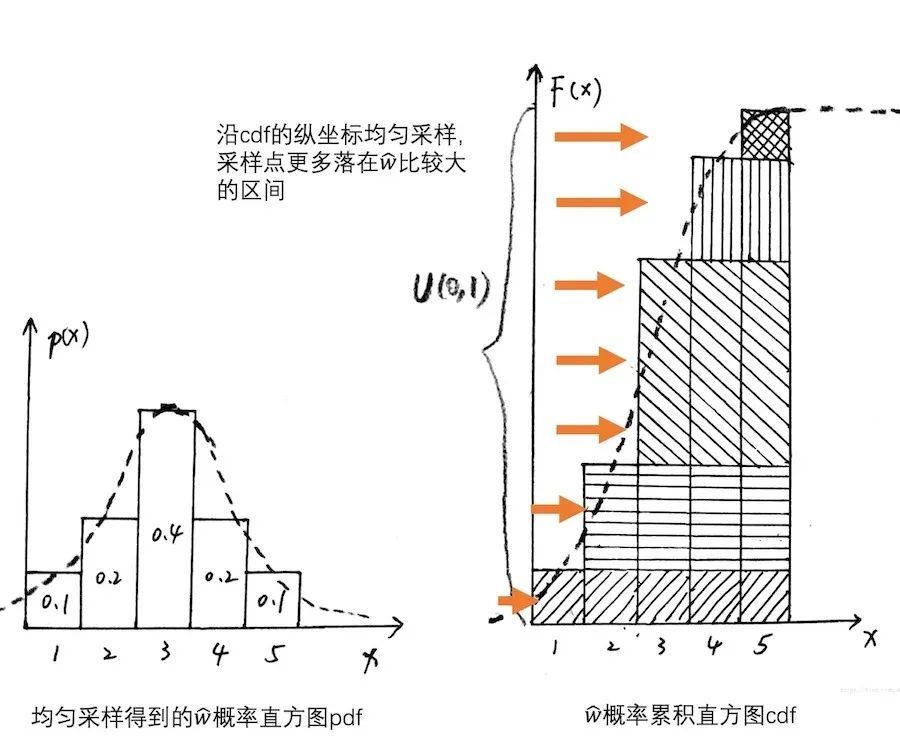Fig. 9：逆变换采样

Reference

[1]Volume Rendering for Developers: Foundations

[2]Models for Direct Volume Rendering

[3]NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

[4]NeRF入门之体渲染 (Volume Rendering)