2DGS-论文笔记

2DGS: 2D Gaussian Splatting for Geometrically Accurate Radiance Fields

项目地址

SIGGRAPH 2024

Fig. 1: Overview

Abstract

3D Gaussian Splatting (3DGS) 最近在辐射场重建领域取得了革命性进展，实现了高质量的新视角合成和快速渲染。然而，由于 3D 高斯的多视图不一致性，3DGS 无法准确表示表面。本文提出了 2D Gaussian Splatting (2DGS)，这是一种从多视图图像中建模和重建几何精确辐射场的新方法。核心思想是将 3D 体积压缩成一组 2D 定向平面高斯盘 (2D oriented planar Gaussian disks)。与 3D 高斯不同，2D 高斯在建模表面时内在地提供了视图一致的几何形状。为了准确恢复薄表面并实现稳定优化，本文介绍了利用光线泼溅交汇 (ray-splat intersection) 和光栅化实现透视准确的 2D splatting 过程。此外，还结合了深度失真 (depth distortion) 和法线一致性项，以进一步提高重建质量。证明了本文的可微渲染器在保持竞争性外观质量、快速训练速度和实时渲染的同时，能够实现无噪声且细节丰富的几何重建。

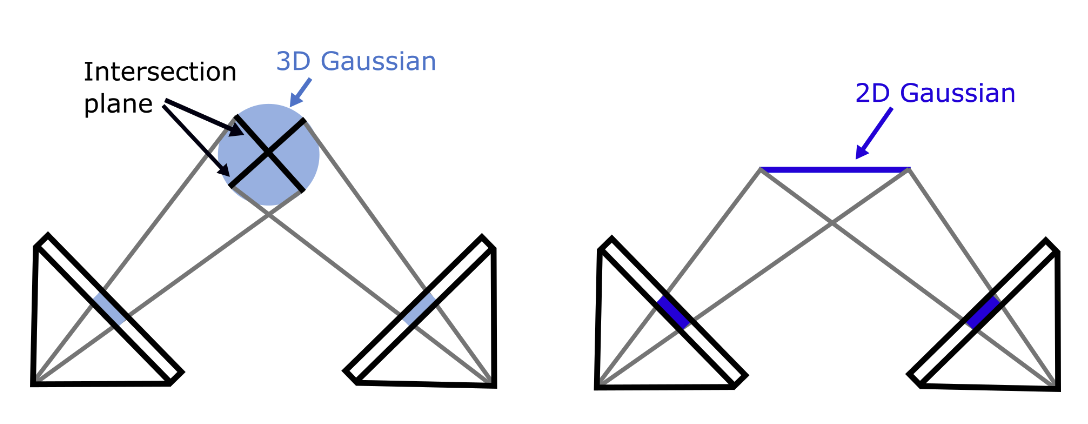
Introduction

因为体积 3D 高斯模型模拟了完整角度的辐射，这与表面的薄性是冲突的。前人的工作已经证明了表面元素 (surfels) 是一个高效表示复杂几何的方法，因此本文用 2D 高斯基元，即定向椭圆盘 (oriented elliptical disk) 来表示 3D 场景。相较于 3D 高斯基元，2D 高斯基元可以准确地表示出物体的表面。如图 2 所示，本文采用显式 ray-splat intersection 的方法。3DGS 通过像素光线的相交处来估计高斯的属性，当视角不同时，会产生不同的交平面，最终会导致不一致性。而 ray-splat intersection 的方法能够实现交汇平面的一致性，最终实现透视正确的 splatting 效果。并且 2D 基元能够很方便地计算出法线。

A surfel, that is, a point structure representing Euclidean xyz coordinates, together with normal coordinates, a RGBA color, a radius, a confidence value and the surface curvature estimate.

Fig. 2: Comparison of 3DGS and 2DGS

如果只是用图片求损失来优化效果并不是非常好，因此本文还引入了深度失真和法线一致性损失。深度失真损失将 2D 基元集中在沿光线分布的一个小范围内，解决了渲染过程中忽略高斯基元之间距离的问题；法线一致性损失能最大限度地减少渲染的法线贴图与渲染的深度梯度之间的差异，确保深度和法线定义的几何图形保持一致。

本文的贡献为：

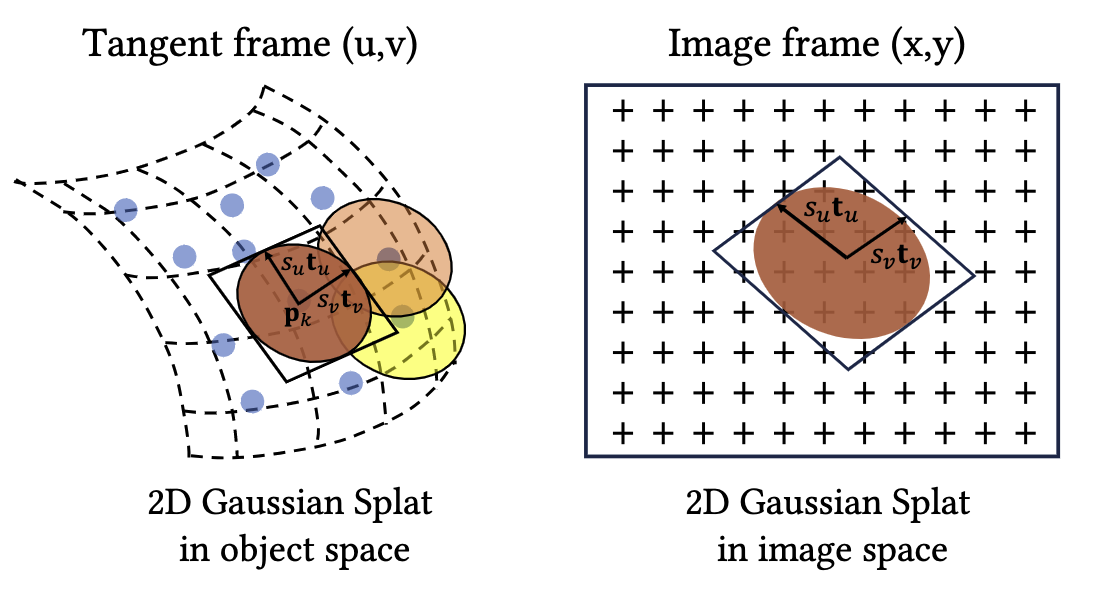
• 提出了一种高效的可微分 2D 高斯渲染器，通过利用 2D 表面建模、ray-splat intersection 和体积积分，实现透视正确的 splatting。
• 引入了两种正则化损失，以改进无噪声表面重建。
• 与其他显式表示法相比，本文的方法实现了最先进的几何重建和新视角生成 (novel view synthesis, NVS) 结果。

Method

Modeling

如图 3 所示，2DGS 以点 $\mathbf{p}_k$ 为中心，有两个主切向量 $\mathbf{t}_u$ 和 $\mathbf{t}_v$ 以及一个控制 2D 高斯方差的缩放向量 $\mathbf{s}=(s_u,s_v)$。两个正交的切向量的叉乘得到高斯基元的法向量 $\mathbf{t}_w=\mathbf{t}_u\times\mathbf{t}_v$。因此可以用一个 $3\times3$ 的旋转矩阵 $\mathbf{R}=[\mathbf{t}_u,\mathbf{t}_v,\mathbf{t}_w]$ 控制基元的方向，用一个最后一行为 $0$ 的 $3\times3$ 对角矩阵 $\mathbf{S}$ 来控制基元的缩放。

Fig. 3: Illustration of 2D Gaussian Splatting

一个定义在局部切平面 (tangent plane) 的 2D 高斯在世界空间中的坐标如下：

$$P(u, v)=\mathbf{p}_k+s_u \mathbf{t}_u u+s_v \mathbf{t}_v v=\mathbf{H}(u, v, 1,1)^{\mathrm{T}} \tag{1}$$

$$\text{where} \ \ \mathbf{H}=\left[\begin{array}{cccc} s_u \mathbf{t}_u & s_v \mathbf{t}_v & \mathbf{0} & \mathbf{p}_k \\ 0 & 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{cc} \mathbf{R S} & \mathbf{p}_k \\ \mathbf{0} & 1 \end{array}\right] \tag{2}$$

• $\mathbf{H}\in4\times4$ 是一个齐次变换矩阵，表示 2D 高斯的几何形状

对于 uv 空间中的点 $\mathbf{u}=(u,v)$，其 2D 高斯的值可以通过标准高斯计算出来：

$$\mathcal{G}(\mathbf{u})=\exp \left(-\frac{u^2+v^2}{2}\right) \tag{3}$$

类似于 3DGS，知道高斯的不透明度 $\alpha$，通过概率密度函数 $\mathcal{G}$，就可以知道每个点的概率密度，进而可以求出每个点的不透明度 $\alpha\mathcal{G}(\mathbf{u})$。所以使用一对正交向量 $\mathbf{t}_u$ 和 $\mathbf{t}_v$ 来定义 2DGS 所在的平面，称为切平面，也就是 uv 空间 (通过公式 1 也能发现 uv 空间以中心为原点)。本文的高斯函数 $\mathcal{G}(\mathbf{u})$ 可以理解为均值为 0，方差为 1 的圆。然后用矩阵 $\mathbf{H}$ 将 uv 空间中的点 $\mathbf{u}(u,v)$ 转换到世界坐标系 (从二维变成三维的点)。

中心 $\mathbf{p}_k$，缩放 $(s_u,s_v)$，旋转 $(\mathbf{t}_u, \mathbf{t}_v)$ 都是可学习的参数，并且和 3DGS 一样， 2D 高斯基元也有不透明度 $\alpha$ 和通过球谐函数计算的视角依赖的外观 $c$。

Splatting

渲染 2D 高斯的常用策略是利用透视投影的仿射变换近似地将 2D 高斯基元投影到屏幕空间，但是这种投影只有在高斯的中心处准确率高，离中心越远误差越大。本文采用基于齐次坐标的计算公式，将 2D splat 的投影过程表示为齐次坐标下一个统一的 2D-to-2D 的映射，简单来说就是直接用齐次变换矩阵将 2D 高斯基元从世界空间投影到屏幕空间。因此屏幕空间中的点可以通过下式进行计算：

$$\mathbf{x}=(x z, y z, z, 1)^{\mathrm{T}}=\mathbf{W} P(u, v)=\mathbf{W H}(u, v, 1,1)^{\mathrm{T}} \tag{4}$$

• $\mathbf{x}$ 表示为从相机发出的穿过像素 $(x,y)$，且与 splat 在深度 $z$ 处相交的齐次光线

对 2D 高斯进行光栅化时，为了找到像素 $(x,y)$ 对应的 uv 坐标，一个简单的想法是可以通过逆变换矩阵 $\mathbf{M}=(\mathbf{W}\mathbf{H})^{-1}$ 来求，即 $\mathbf{u}=\mathbf{M}\mathbf{x}$。但是这个逆变换矩阵带来了数值的不稳定性，特别是当从侧面观察 splat 退化为线段时。以前的一些方法会设定一个阈值，当 splat 退化到一定程度时就不再使用这个变换，但这又会使得可微渲染的优化过程不稳定。为了解决这个问题，2DGS使用了一个显式的 ray-splat intersection。

通常来说屏幕空间应该用 uv 表示，但是在前文的局部切平面已经用 uv 表示了，所以本文用 xy 来表示屏幕空间。$\mathbf{H}$ 矩阵是从 uv 空间变换到世界空间，$\mathbf{W}$ 矩阵是从世界空间变换到屏幕空间。

Ray-splat Intersection. Ray-splat Intersection 就是通过找 3 个非平行平面的交点来确定像素 $(x,y)$ 对应的 uv 坐标。具体来说就是在屏幕空间内用两个正交的平面来确定像素点 $\mathbf{x}=(x,y)$，两个平面分别是平行于 x 轴的 x-plane $\mathbf{h}_x=(-1,0,0,x)^T$ 和平行于 y 轴的的 y-plane $\mathbf{h}_y=(0,-1,0,y)^T$，这两个平面是用 4D 齐次平面表示。

4D 齐次平面方程为 $ax+by+cz+dw=0$，可以理解为 $(x,y,z,w)$ 是在 4D齐次平面 $(a,b,c,d)$ 上的点，因此可以参数化这个平面为 $\mathbf{h}=(a,b,c,d)$。对于与 x 轴平行的平面，假设为 $x=x_0$，那么该平面上的点一般用齐次坐标表示为 $(x_0,y,z,1)$，平面 $(a,b,c,d)$ 要满足 $ax_0+by+cz+d=0$，所以该 4D 齐次平面可以表示为 $(-1,0,0,x_0)$。

然后就是要将这两个平面变换到 uv 空间。用变换矩阵 $\mathbf{M}$ 对平面上一个点进行变换，等同于用 $\mathbf{M}^{-T}$ 对整个齐次平面进行变换。因此可以用 $(\mathbf{WH})^T$ 找到像素 $(x,y)$ 对应的 uv 坐标，等价于用前面逆变换矩阵 $\mathbf{M}=(\mathbf{W}\mathbf{H})^{-1}$，并且这么做省去了求逆的过程：

$$\mathbf{h}_u=(\mathbf{W H})^{\mathrm{T}} \mathbf{h}_x \quad \mathbf{h}_v=(\mathbf{W H})^{\mathrm{T}} \mathbf{h}_y \tag{5}$$

这里只用到了 2 个平面，第三个平面就是 2D 高斯基元的平面。x-plane 和 y-plane 的交线表示的是从相机发出的穿过像素 $(x,y)$ 的光线，最终与 2D 高斯基元平面相交于一个点，这个点其实就是最终要找的 uv 空间中的点 $\mathbf{u}=(u,v)$，可以通过以下等式确定这个点：

$$\mathbf{h}_u\cdot(u,v,1,1)^\mathrm{T}=\mathbf{h}_v\cdot(u,v,1,1)^\mathrm{T}=0 \tag{6}$$

首先用齐次坐标 $(u,v,1,1)$ 表示该点一定上 2D 高斯基元平面上，公式 6 又表示该点又同时在 x-plane 和 y-plane 上，因此这个点就是这三个平面的唯一交点。

通过公式 6 最终可以解出交点的 uv 坐标：

$$u(\mathbf{x})=\frac{\mathbf{h}_u^2 \mathbf{h}_v^4-\mathbf{h}_u^4 \mathbf{h}_v^2}{\mathbf{h}_u^1 \mathbf{h}_v^2-\mathbf{h}_u^2 \mathbf{h}_v^1} \quad v(\mathbf{x})=\frac{\mathbf{h}_u^4 \mathbf{h}_v^1-\mathbf{h}_u^1 \mathbf{h}_v^4}{\mathbf{h}_u^1 \mathbf{h}_v^2-\mathbf{h}_u^2 \mathbf{h}_v^1} \tag{7}$$

• $\mathbf{h}^i_u,\mathbf{h}^i_v$ 表示 4D 齐次平面的第 $i$ 个参数

通过公式 4 可以得到深度 $z$，通过公式 3 可以得到高斯的值。

总结一下 2DGS 的光栅化过程：屏幕空间中的一个像素 $\mathbf{x}=(x,y)$ 首先通过公式 7 可以确定其在 uv 空间中的坐标 $\mathbf{u}(\mathbf{x})=(u,v)$，然后再根据公式 1 可以得到其在世界空间中的坐标 $P(u,v)=(x,y,z)$。

Degenerate Solutions. 从一些很斜的角度看，2D 高斯会退化成一条线，在光栅化的过程中会消失。为了解决这个问题，本文使用 uv 空间的低通滤波：

$$\hat{\mathcal{G}(\mathbf{x})}=\max\left\{\mathcal{G}(\mathbf{u}(\mathbf{x})),\mathcal{G}\left(\frac{\mathbf{x}-\mathbf{c}}{\sigma}\right)\right\} \tag{8}$$

• $\mathbf{u}(\mathbf{x})$ 表示通过公式 7 计算出来的 uv 坐标
• $\mathbf{c}$ 表示投影后的中心点 $\mathbf{p}_k$

通俗地来说，当 2D 高斯在屏幕空间比半径为 $\sigma$ 的圆还要小的时候，就把它当成半径为 $\sigma$ 的圆。本文取 $\sigma=\sqrt{2}/2$

Rasterization. 光栅化的过程和 3DGS 一样，也是用 alpha 混合的算法：

$$\mathbf{c}(\mathbf{x})=\sum_{i=1} \mathbf{c}_i \alpha_i \hat{\mathcal{G}}_i(\mathbf{u}(\mathbf{x})) \prod_{j=1}^{i-1}\left(1-\alpha_j \hat{\mathcal{G}}_j(\mathbf{u}(\mathbf{x}))\right) \tag{9}$$

Training

Depth Distortion. NeRF 是在光线上进行采样，因此会考虑采样点之间的距离，而 3DGS 的体渲染并没有考虑高斯基元之间的距离。在光线方向有重叠的高斯基元之间的距离不同，也可能会产生相似的渲染结果。并且和传统的表面渲染不同，表面渲染只需要渲染与光线相交的第一个表面即可，而体渲染需要对光线上所有的高斯基元进行累加。为了解决这个问题，本文使用了深度失真来最小化 ray-splat intersections 之间的距离来集中权重的分布：

$$\mathcal{L}_d = \sum_{i,j} \omega_i \omega_j \left| z_i - z_j \right | \tag{10}$$

• $\omega_i = \alpha_i \hat{\mathcal{G}}_i (\mathbf{u}(\mathbf{x})) \prod_{j=1}^{i-1} \left(1 - \alpha_j \hat{\mathcal{G}}_j (\mathbf{u}(\mathbf{x})) \right)$ 表示光线上第 $i$ 个交点的混合权重
• $z_i$ 表示交点的深度

从这个公式也能看出高斯基元的不透明度越高，权重也越高，所以这个公式可以理解为减少具有高不透明度基元之间的深度差异。并且这个正则项是通过 CUDA 实现的。

在补充材料中还有对公式 10 进行补充：

$$\begin{aligned} \mathcal{L} & =\sum_{i=0}^{N-1} \sum_{j=0}^{i-1} \omega_i \omega_j\left(m_i-m_j\right)^2 \\ & =\sum_{i=0}^{N-1} \omega_i\left(m_i^2 \sum_{j=0}^{i-1} \omega_j+\sum_{j=0}^{i-1} \omega_j m_j^2-2 m_i \sum_{j=0}^{i-1} \omega_j m_j\right) \\ & =\sum_{i=0}^{N-1} \omega_i\left(m_i^2 A_{i-1}+D_{i-1}^2-2 m_i D_{i-1}\right), \end{aligned} \tag{11}$$

• $m_i$ 表示 NDC 空间下第 $i$ 个高斯基元的深度
• $A_i=\sum_{j=0}^i \omega_j$ 表示前 $i$ 个高斯基元的不透明度权重之和
• $D_i^2=\sum_{j=0}^i \omega_j m_j^2$ 表示前 $i$ 个高斯基元的深度权重平方之和
• $D_i=\sum_{j=0}^i \omega_j m_j$ 表示前 $i$ 个高斯基元的深度权重之和

令 $e_i=m_i^2 A_{i-1}+D_{i-1}^2-2 m_i D_{i-1}$， $e_i$ 表示的是直到第 $i$ 个高斯基元的深度失真量。深度失真损失可以像 alpha 混合一样用 $\mathcal{L}_i=\sum^i_{j=0}\omega_je_j$ 来渲染深度失真。

Normal Consistency. 因为光线上可能存在很多半透明的点，因此把累积不透明度达到 $0.5$ 的交点 $\mathbf{p}_s$ 作为真实表面。通过下面这个损失函数将表面的法线与深度图的梯度算出来的法线对齐：

$$\mathcal{L}_n=\sum_i\omega_i(1-\mathbf{n}_i^T\mathbf{N}) \tag{12}$$

• $\omega_i$ 和公式 10 一样
• $\mathbf{n}_i$ 表示光线上第 $i$ 个基元的法线
• $\mathbf{N}$ 表示深度图的梯度估计出来的法线

$\mathbf{N}$ 是通过相邻点的深度的有限差分算出来的：

$$\mathbf{N}(x, y) = \frac{\nabla_x \mathbf{p}_s \times \nabla_y \mathbf{p}_s}{|\nabla_x \mathbf{p}_s \times \nabla_y \mathbf{p}_s|} \tag{13}$$

这样就可以使 2D 高斯基元尽可能分布在物体的表面上。

最终总的损失函数为：

$$\mathcal{L}=\mathcal{L}_c+\lambda_d\mathcal{L}_d+\lambda_n\mathcal{L}_n \tag{14}$$

• $\mathcal{L}_c$ 表示结合 $\mathcal{L}_1$ 损失和 D-SSIM 损失的 RGB 损失

Reference

[1]2D Gaussian Splatting for Geometrically Accurate Radiance Fields

[2]2D Gaussian Splatting论文阅读笔记

[3]新风向？——2DGS（2D高斯泼溅）横空出世

[4][NeRF坑浮沉记]3DGS的升级？2DGS文献阅读笔记：Gaussian的光栅化

[5]2DGS中的参数化

[6]2DGS的非官方实现以及相关推导