SAGA-论文笔记

Segment Any 3D Gaussians

项目地址

arXiv preprint arXiv:2312.00860 (这里看的是 v1 版本)

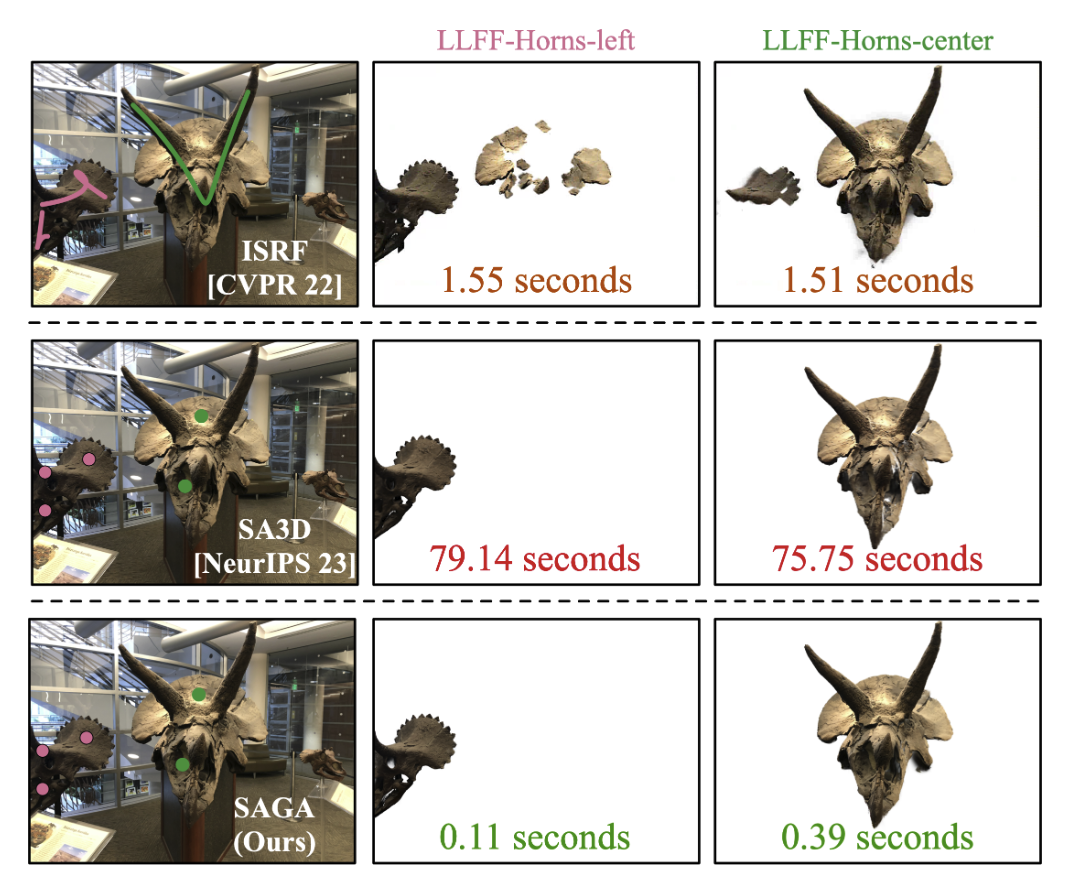
Fig. 1: Overview

Abstract

在辐射场中进行交互式 3D 分割是一项很有吸引力的任务，因为它对 3D 场景的理解和操作非常重要。然而，现有的方法在实现细粒度、多粒度分割方面面临着挑战，或者要与巨大的计算开销作斗争，从而阻碍了实时交互。本文介绍了 Segment Any 3D GAussians (SAGA)，这是一种新颖的 3D 交互式分割方法，它将 2D 分割基础模型与 3DGS 无缝融合在一起。SAGA 通过精心设计的对比训练，将由分割基础模型生成的多粒度 2D 分割结果有效地嵌入到 3D 高斯点特征中。对现有 benchmarks 的评估表明，SAGA 的性能可与最先进的方法相媲美。此外，SAGA 还能实现多粒度分割，并适应各种提示，包括点、涂鸦和 2D mask。值得注意的是，SAGA 可以在几毫秒内完成 3D 分割，与之前的 SOTA 相比，实现了近 1000 倍的加速。

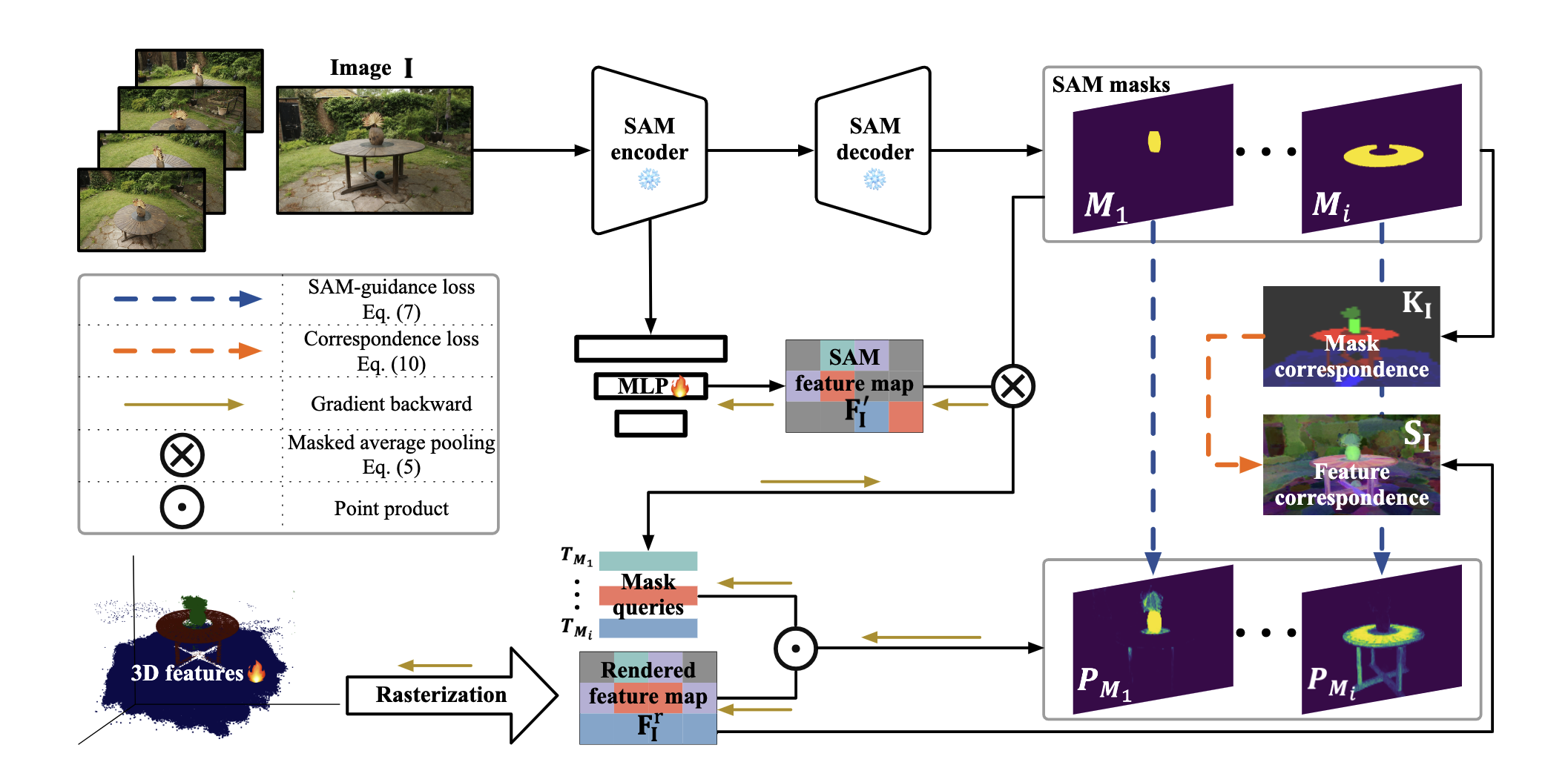
Method

Fig. 2: Pipeline

Preliminary

3D Gaussian Splatting (3DGS)：这部分直接跳过。

Segment Anything Model (SAM)：输入图片 $\mathbf{I}$ 和一组提示 $\mathcal{P}$，输出对应 2D 分割 mask $\mathbf{M}$：

$$\mathbf{M}=\mathrm{SAM}(\mathbf{I},\mathcal{P}) \tag{1}$$

Overall Pipeline

如图 2 所示，给定一个预训练 3DGS 模型 $\mathcal{G}$ 和其训练集 $\mathcal{I}$，首先用 SAM encoder 对训练集 $\mathcal{I}$ 中的每张图片 $\mathbf{I}\in\R^{H\times W}$ 提取 2D 特征图 $\mathbf{F}_{\mathbf{I}}^{\mathrm{SAM}}\in\R^{C^{\mathrm{SAM}}\times H\times W}$ 和一组多粒度 mask $\mathcal{M}^{\mathrm{SAM}}_{\mathbf{I}}$。然后对 $\mathcal{G}$ 中的每个高斯基元 $\mathbf{g}$ 基于提取出来的 mask 训练一个低维特征 $\mathbf{f}_{\mathbf{g}}\in\R^{C}$ 来聚集这些多视角多粒度的分割信息 ($C$ 表示特征的维度，默认为 32)。

在推理的阶段，对于一个特定视角，有相机位姿 $v$ 和基于输入的提示 $\mathcal{P}$ 生成的一组查询 $\mathcal{Q}$。通过与所学特征的高效特征匹配，利用这些查询来检索对应的 3D 高斯。此外，还引入了一种高效的后处理操作，利用 3DGS 的点云结构提供的强大 3D 先验来完善检索到的 3D 高斯。

Training Features for Gaussians

给定一张带有特定相机位姿 $v$ 的训练图像 $\mathbf{I}$，我们首先根据预先训练好的 3DGS 模型 $\mathcal{G}$ 渲染相应的特征图。像素 $p$ 渲染出来的特征 $\mathbf{F}^r_{\mathbf{I},p}$ 为：

$$\mathbf{F}_{\mathbf{I}, p}^r=\sum_{i \in \mathcal{N}} \mathbf{f}_i \alpha_i \prod_{j=1}^{i-1}\left(1-\alpha_j\right) \tag{2}$$

• $\mathcal{N}$ 表示该像素上重叠的高斯基元的有序集合

在训练阶段，冻结 3D 高斯的其他所有参数。

SAM-guidance Loss：通过 SAM 自动提取的 2D mask 十分复杂且容易混淆 (即三维空间中的一个点在不同视角上可能被分割为不同的物体)。为了解决这个问题，本文提出用 SAM 生成的 features 来 guidance。如图 2 所示，首先用 MLP $\varphi$ 把 SAM features 投影到与 3D features 相同的低维空间：

$$\mathbf{F}_{\mathrm{I}}^{\prime}=\varphi\left(\mathbf{F}_{\mathrm{I}}^{\mathrm{SAM}}\right) \tag{3}$$

然后对于 mask 集合 $\mathcal{M}^{\mathrm{SAM}}_{\mathbf{I}}$ 中的每个 $\mathbf{M}$，通过 masked average pooling 的操作得到相应的查询 $\mathbf{T}_\mathbf{M}\in\R^C$：

$$\mathbf{T}_{\mathbf{M}}=\frac{1}{\|\mathbf{M}\|_1} \sum_{p=1}^{H W} \mathbb{1}\left(\mathbf{M}_p=1\right) \mathbf{F}_{\mathbf{I}, p}^{\prime} \tag{4}$$

• $\mathbb{1}$​ 表示指示函数

就是求 mask 区域特征的均值作为这个 segmentation 的特征值，是个单位向量。

然后 $\mathbf{T}_\mathbf{M}$ 通过 softmaxed point product 来分割 rendered feature map：

$$\mathbf{P}_\mathbf{M}=\sigma(\mathbf{T}_\mathbf{M}\cdot\mathbf{F}_\mathbf{I}^r) \tag{5}$$

• $\sigma$​ 表示逐元素的 sigmoid 函数

因为特征值是单位向量，所以进行点乘就是求余弦相似度，这里就是在算 rendered feature map 的每个像素和哪个特征值最接近，本质上就是在看这个像素是属于哪个 segmentation。

SAM-guidance loss 被定义为分割结果 $\mathbf{P}_\mathbf{M}$ 与相应 SAM 提取的 mask $\mathbf{M}$ 之间的二值交叉熵：

$$\mathcal{L}_{\mathrm{SAM}}= -\sum_{\mathbf{I} \in \mathcal{I}} \sum_{\mathbf{M} \in \mathcal{M}_{\mathbf{I}}} \sum_p^{H W}\left[\mathbf{M}_p \log \mathbf{P}_{\mathbf{M}, p}\right. \left.+\left(1-\mathbf{M}_p\right) \log \left(1-\mathbf{P}_{\mathbf{M}, p}\right)\right] \tag{6}$$

Correspondence Loss：考虑到一个像素 $p$ 可能同时属于 mask 集合 $\mathcal{M}_{\mathbf{I}}$ 中的一个子集 $\mathcal{M}_{\mathbf{I}}^{p}$，假设 $p_1,p_2$ 分别属于 mask 集合 $\mathcal{M}_{\mathbf{I}}^{p_1},\mathcal{M}_{\mathbf{I}}^{p_2}$，当两个集合的交集和并集的比值越大，说明这两个像素的特征值也越相似，因此 mask correspondence 定义为：

$$\mathbf{K}_{\mathbf{I}}\left(p_1, p_2\right)=\frac{\left|\mathcal{M}_{\mathbf{I}}^{p_1} \cap \mathcal{M}_{\mathbf{I}}^{p_2}\right|}{\left|\mathcal{M}_{\mathbf{I}}^{p_1} \cup \mathcal{M}_{\mathbf{I}}^{p_2}\right|} \tag{7}$$

feature correspondence $\mathbf{S}_{\mathbf{I}}(p_1,p_2)$ 被定义为其 rendered features 之间的余弦相似度：

$$\mathbf{S}_{\mathbf{I}}(p_1,p_2)=<\mathbf{F}_{\mathbf{I},p_1}^r,\mathbf{F}_{\mathbf{I},p_2}^r> \tag{8}$$

最后 correspondence loss 定义为：

$$\mathcal{L}_{\text {corr }}=-\sum_{\mathbf{I} \in \mathcal{I}} \sum_{p_1}^{H W} \sum_{p_2}^{H W} \mathbf{K}_{\mathbf{I}}\left(p_1, p_2\right) \mathbf{S}_{\mathbf{I}}\left(p_1, p_2\right) \tag{9}$$

如果两个像素从来没有属于同一个分割的话，就令 $\mathbf{K}_\mathbf{I}=-1$ 来减少特征相似度。

最后 SAGA 的 loss 为：

$$\mathcal{L}=\mathcal{L}_{\mathrm{SAM}}+\lambda\mathcal{L}_{\mathrm{corr}} \tag{10}$$

• 本文默认 $\lambda=1$​

3D Prior Based Post-processing

原始分割出来的 3D 高斯 $\mathcal{G}^t$​ 存在两个问题：(i) 存在多余的噪声；(ii) 有些属于这个物体的高斯基元没有被分割出来；为了解决这两个问题，引入了穿透点云分割中的两种技术——统计滤波算法 (Statistical Filtering) 和区域增长算法 (Region Growing)。

Statistical Filtering：两个高斯基元之间的距离可以推断出他们是否属于同一个物体，统计滤波先用 K 最近邻 (K-Nearest Neighbors, KNN) 算法计算每个高斯基元与最近的 $\sqrt{|\mathcal{G}^t|}$ 个高斯基元之间的平均距离。然后计算所有平均距离的均值 $\mu$ 和方差 $\sigma$，对于平均距离超出 $\mu+\sigma$ 的点就过滤掉，最后得到 $\mathcal{G}^{t'}$。

Region Growing Based Filtering：2D mask 可以作为目标正确位置的先验，首先将 mask 投影到分割出来的高斯基元 $\mathcal{G}^t$ 上，得到一个 validated 子集 $\mathcal{G}^c$，对于 $\mathcal{G}^c$ 中的每个高斯基元，计算和其相邻最近高斯基元的欧拉距离 $d_g$​：

$$d_{\mathbf{g}}^{\mathcal{G}^c}=\min \left\{D\left(\mathbf{g}, \mathbf{g}^{\prime}\right) \mid \mathbf{g}^{\prime} \in \mathcal{G}^c\right\} \tag{11}$$

找到欧拉距离的最大值 $\max\{d_{\mathbf{g}}^{\mathcal{G}^c}|\mathbf{g}\in\mathcal{G}^c\}$。然后开始迭代，从 $\mathcal{G}^t$ 中选择高斯基元并判断是否要加入到 $\mathcal{G}^c$ 中，如果 $\mathcal{G}^t$ 中的高斯基元与 $\mathcal{G}^c$ 中任意一个高斯基元的欧拉距离小于前面找到的那个最大值，就将其加入到 $\mathcal{G}^c$ 中。当区域增长算法收敛后，就得到了新的分割结果 $\mathcal{G}^{t'}$​。

Ball Query Based Growing：对于之前提到的问题 (ii)，本文采用 ball query 算法从所有的高斯基元 $\mathcal{G}$ 中查找需要的高斯基元。以 $\mathcal{G}^{t'}$ 中每个高斯基元为中心，$r$ 为半径的的球形邻域内所有的高斯基元都被加入到最终的分割结果 $\mathcal{G^s}$ 中，半径 $r=\max\{d_{\mathbf{g}}^{\mathcal{G}^{t'}}|\mathbf{g}\in\mathcal{G}^{t'}\}$。

Reference

[1]Segment Any 3D Gaussians