HumanSplat-论文笔记

HumanSplat: Generalizable Single-Image Human Gaussian Splatting with Structure Priors

项目地址

NeurlPS 2024

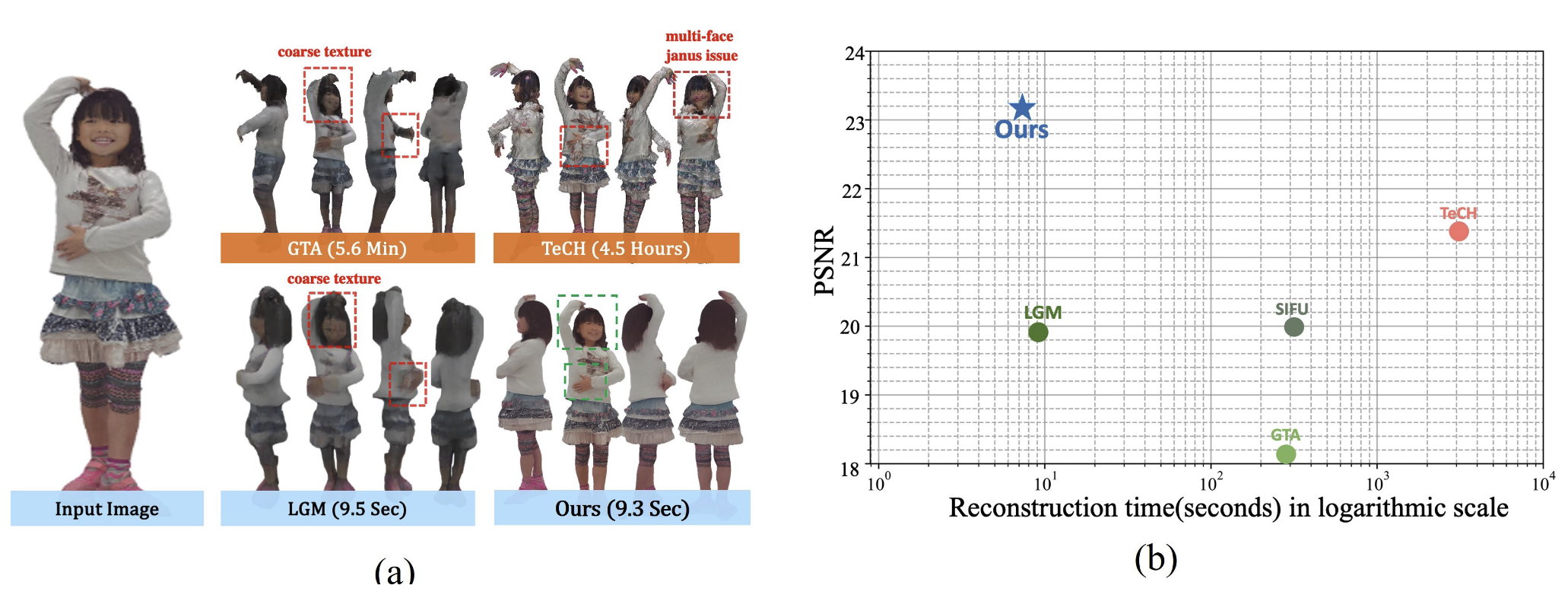
Fig. 1: Overview

Abstract

尽管高保真人体重建技术取得了最新进展，但通常需要大量的输入图像或优化时间，这极大地阻碍了它们在更广泛的场景中的应用。为了解决这些问题，我们提出了 HumanSplat，它以生成的方式从单个输入图像预测任何人的 3DGS 属性。具体来说，HumanSplat 包括一个 2D 多视角扩散模型和一个具有人体结构先验的潜在重建 Transformer，能够巧妙地将几何先验和语义特征整合在统一框架中。此外，我们设计了一个分层损失，结合了人体语义信息，以实现高保真的纹理建模，并更好地约束估计的多视角。标准 benchmarks 和真实场景图像上的综合实验表明，HumanSplat 在实现逼真的新视角合成方面超越了现有的 SOTA。

Introduction

本文的主要贡献：

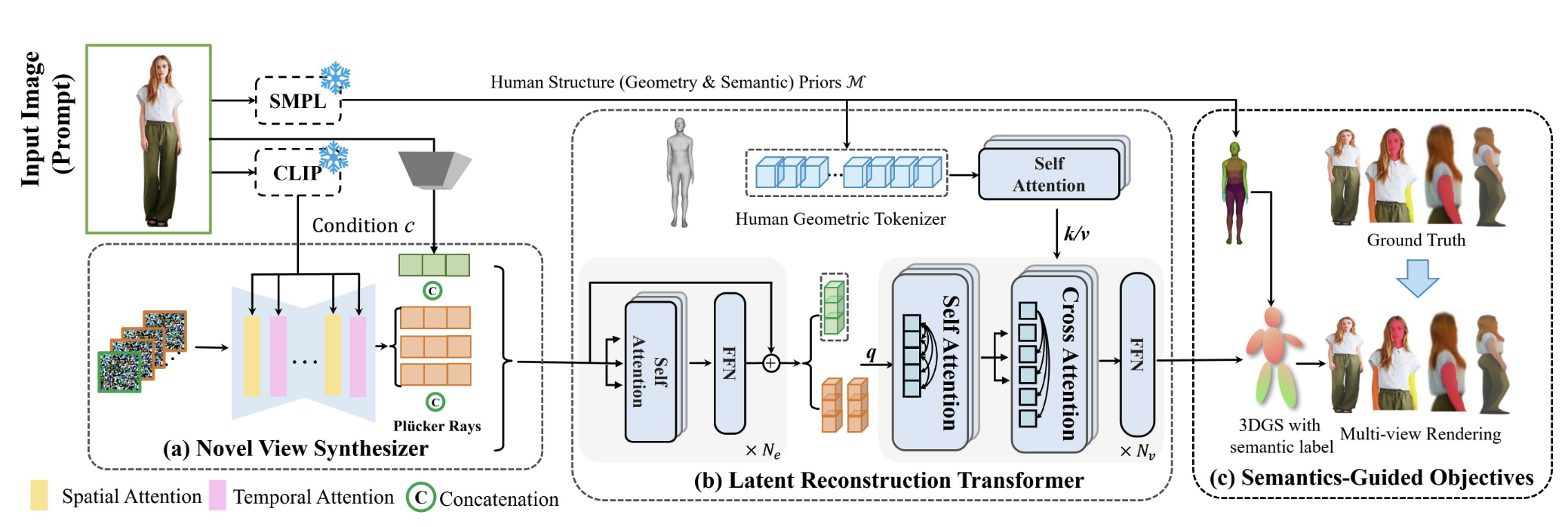
• 我们提出了一种新颖的可通用人体 GS 网络，用于从单张图像进行高保真人体重建
• 我们通过利用来自 SMPL 模型的人体几何先验和来自 2D 生成扩散模型的人体外观先验，将结构和外观信息整合到一个通用的Transformer框架中。几何先验有助于稳定生成高质量的人体几何结构，而外观先验则有助于推测穿衣人体的未见部分。
• 我们通过引入语义提示、分层监督和定制的损失函数，提升了重建人体模型的保真度。

Method

Fig. 2: Pipeline

Overview

首先先预测出人体 SMPL 模型的几何先验证 $\mathcal{M}$，并用 CLIP 得到输入图像的 embedding $\mathbf{c}$。微调视频扩散模型SV3D——多视角生成器(novel-view synthesizer) 生成多视角的 latent features $\{\mathbf{F}_i\in\R^{h\times w\times c}\}^{\mathbf{N}}_{i=1}$，其中 $\mathbf{N}$ 表示视角的数量，$h,w$ 和 $c$ 是 latent features 的高，宽和通道数 (图 2a)。然后用一个新的 latent reconstruction transformer 将人体几何先验和 latent features 集中在一个统一的架构内来预测高斯的属性 $\mathbf{G}:=\left\{\left(\boldsymbol{\mu}_i, \boldsymbol{q}_i, \boldsymbol{s}_i, \boldsymbol{c}_i, \boldsymbol{\sigma}_i\right) \mid i=1, \ldots, \mathbf{N}_{\mathbf{p}}\right\}$，其中 $\mathbf{N_p}$ 表示高斯点云的数量 (图 2b)。为了实现高保真纹理建模和更好地约束预测出来的多视角结构，设计了一种结合了人类语义先验的分层损失 (图 2c)。

Video Diffusion Model as Novel-view Synthesizer

SV3D 以通过 CLIP 得到输入图像 $\mathbf{I}_0$ 的 embedding $\mathbf{c}$ 和通过预训练 VQ-VAE $\mathcal{E}$ 得到的 $\mathbf{I}_0$ 的 latent feature $\mathbf{F}_0$ 作为条件，通过一个 spatial-temporal UNet $D_\theta$，将高斯噪声逐步去噪为时间连续的 $N$ 个多视角 latent feature $\{\mathbf{F}_i\}^N_{i=1}$：

$$\mathbb{E}_{\epsilon \sim p(\epsilon)}\left[\lambda(\epsilon)\left\|D_\theta\left(\left\{\mathbf{F}_i^\epsilon\right\}_{i=1}^{\mathbf{N}} ; \mathbf{c}, \mathbf{F}_0, \epsilon\right)-\left\{\mathbf{F}_i\right\}_{i=1}^{\mathbf{N}}\right\|_2^2\right] \tag{1}$$

• $\{\mathbf{F}_i^\epsilon\}$ 表示有噪声的多视角 latent features
• $p(\epsilon)$ 表示噪声概率分布
• $\lambda(\epsilon)\in\R^+$ 表示与噪声水平 $\epsilon$ 相关的损失权重项

本文用人体数据集对 SV3D 进行微调以提升其在人体重建方面的能力。

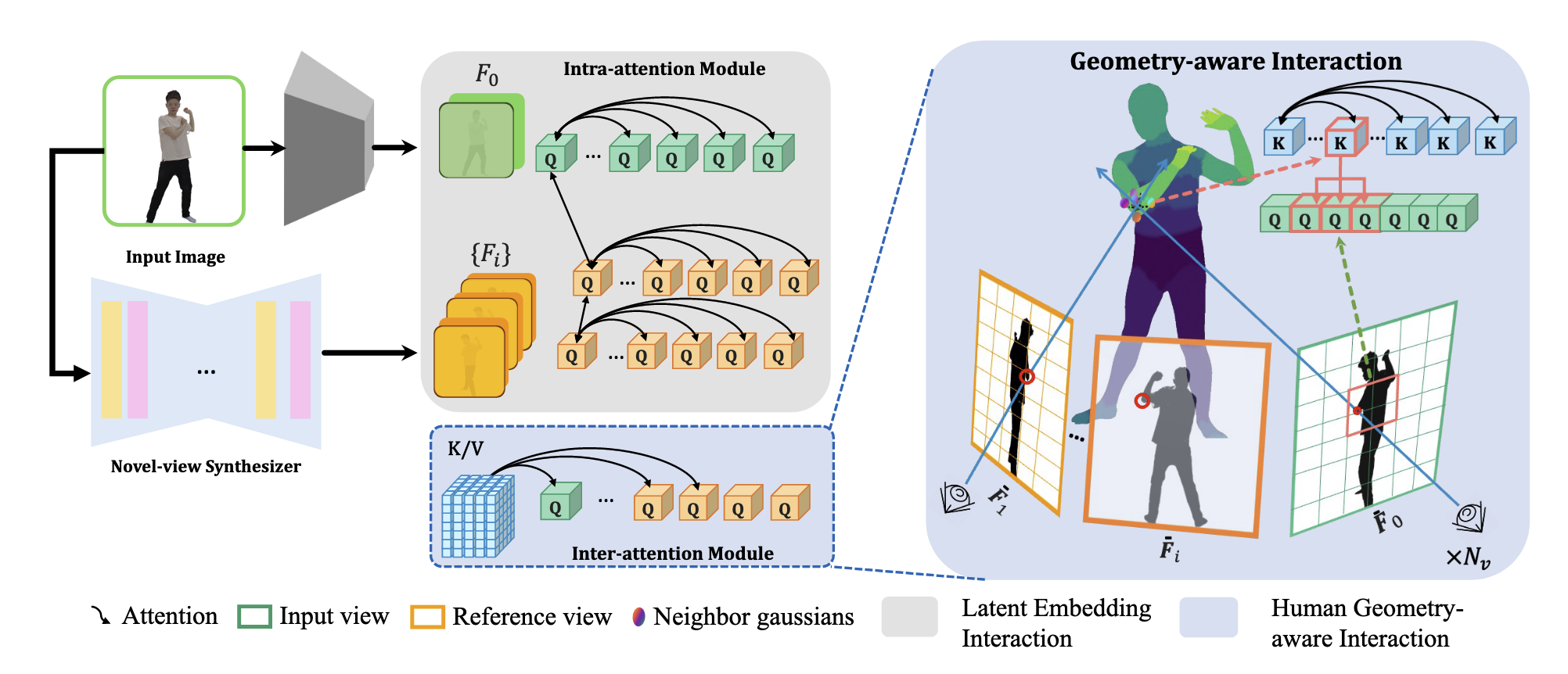
Latent Reconstruction Transfomer

Fig. 3: Illustration of latent reconstruction transformer

这一部分就是将从视频扩散模型中得到的 latent features 和人体几何先验集成在一起。

Latent Embedding Interaction

将输入图片的 latent features $\mathbf{F}_0=\mathcal{E}(\mathbf{I_0})\in\R^{h\times w \times c}$，生成新视角下图片的 latent features $\{\mathbf{F}_i^\epsilon\}_{i=1}^\mathbf{N}$ 以及普吕克坐标进行 concatenation。然后将这些 latents 分成不重叠的 patches 并通过线性层映射成 d 维的 latent tokens。最后通过 intra-attention 模块充分提取 latent tokens 中的空间关联，该模块通过标准的 Transformer 实现，包含多层多头自注意力和前馈网络 (FFN)：

$$\overline{\mathbf{F}}_0, \overline{\mathbf{F}}_1, \ldots, \overline{\mathbf{F}}_{\mathbf{N}}=\operatorname{FFN}\left(\operatorname{SelfAttention}\left(\mathbf{F}_0, \mathbf{F}_1, \ldots, \mathbf{F}_{\mathbf{N}}\right)\right) \tag{2}$$

普吕克坐标是用 6 维向量唯一表示 3D 空间中的一条线，具体是怎么表示可以看这篇文章。每个像素对应相机发出的一条光线，有一个普吕克坐标。本质上就是相机位姿的特征图，把相机位姿作为 condition。

Geometry-aware Interaction

Human Geometric Tokenizer. 这一部分是为了得到空间坐标 $x\in \R^3$ 处的特征向量。给出人体几何模型 $\mathcal{M}\in\R^{6890\times 3}$ 和相机参数，将 $x$ 投影到 2D 图像上，通过对 feature grids 进行双线性插值得到特征向量：

$$\boldsymbol{\Pi}_i(x)=\mathbf{K}(\mathbf{R}\mathcal{M}_i+\mathbf{t}) \tag{3}$$

• $\mathbf{R}$ 和 $\mathbf{t}$ 是相机外参，$\mathbf{K}$ 是相机内参

将 $x$ 和 $\mathbf{F}_0(\boldsymbol{\Pi}(x))$ 进行 concatenate 并映射到 d 维得到人体几何先验 tokens。通过 intra-attention 模块得到几何特征 $\bar{\mathbf{H}}_i\in\R^{6890\times d}$。

Human Geometry-aware Attention.

通常直接使用 SMPL 模型作为先验是包含一定的误差的，因为 SMPL 不包含衣服的建模。为了解决人体先验方面的误差，本文将 3D tokens 投射到 2D 空间，然后查询 2D 空间到邻接窗口 (图 3)。具体来说，在 inter-attention 模块中引入 project-aware attention，在窗口 $\mathbf{W}(k_{win}\times k_{win})$ 内使用 masked 的多头注意力机制。latent features $\{\bar{\mathbf{F}}_i\}$ 作为 queries，人体先验 tokens $\{\bar{\mathbf{H}}_i\}$ 作为 keys/values：

$$\tilde{\mathbf{F}}_i=\operatorname{FFN}(\operatorname{CrossAttention}_{mask}(\bar{\mathbf{F}}_i,\bar{\mathbf{H}}_i)) \tag{4}$$

只有当 $\boldsymbol{\Pi}(\bar{\mathbf{H}}_i,\mathbf{K},\mathbf{R},\mathbf{t})$ 在窗口 $\bar{\mathbf{F}}_i$ 内的时候才会进行特征交互。和标准的交叉注意力机制不同，因为窗口的存在，复杂度从 $\mathcal{O}(\mathbf{L}_F\times \mathbf{L}_H)$ 降为 $\mathcal{O}(\mathbf{L}_F \times k^2_{win})$，其中 $\mathbf{L}_F$ 和 $\mathbf{L}_H$ 分别表示 latent 和 人体先验 tokens 的长度。

Semantics-guided Objectives

对于输出的 token $\tilde{\mathbf{F}}_i$，通过一个 $1\times1$ 的卷积层解码出高斯的属性，每个 patch 都是按像素对齐的方式进行解码。

Hierarchical Loss. 传统方法总是忽视人体包含的丰富的语义信息，本文提出了一个新的框架，利用语义线索、分层监督和定制的损失函数来指导训练过程。基于人体先验模型的丰富语义信息，建立起 3D 空间位置与人体部位之间的对应关系。因此，可以针对不同的身体部位使用不同的注意力权重，并从不同的视角渲染不同级别的 GT 图像以提供分层监督。这种方法极大地促进了基本身体部位的精确定位，包括头部、手和手臂。总损失定义为特定部分损失的加权和：

$$\mathcal{L}_{\mathcal{H}}=\frac{1}{l} \frac{1}{n} \sum_{i=1}^n \sum_{j=1}^m \lambda_i \lambda_j \mathcal{L}_{R e c}\left(\mathbf{I}_{\mathrm{part}, j}, \hat{\mathbf{I}}_{\mathrm{part}, j}\right) \tag{5}$$

• $i\in\{1,...,n\}$ 和 $j\in\{1,...,m\}$ 分别表示不同分辨率的级别和不同的人体部分
• $\hat{\mathbf{I}}_{\mathrm{part}, j}$ 和 $\mathbf{I}_{\mathrm{part}, j}$ 分别表示 $j$ 部分预测的数据和 GT 数据
• $\lambda_i$ 和 $\lambda_j$ 分别表示不同分辨率和不同身体部分的权重

Reconstruction Loss. 基于 $\mathbf{N}_{render}$ 个渲染出来的多视角图片的重建损失函数为：

$$\mathcal{L}_{R e c}=\sum_i^{\mathbf{N}_{\text {render }}} \mathcal{L}_{m s e}\left(\hat{\mathbf{I}}_i, \mathbf{I}_i\right)+\lambda_m L_{m s e}\left(\hat{\mathbf{M}}_i, \mathbf{M}\right)+\lambda_p \mathcal{L}_p\left(\hat{\mathbf{I}}_i, \mathbf{I}_i\right) \tag{6}$$

• $\mathbf{I}_i$ 和 $\hat{\mathbf{I}}_i$ 分别表示 GT 图片和通过 GS 渲染出来的图片
• $\mathbf{M}_i$ 和 $\hat{\mathbf{M}}_i$ 分别表示原始的和渲染出来的前景 mask
• $\mathcal{L}_{mse}$ 表示 MSE loss
• $\mathcal{L}_{p}$ 表示 perceptual loss

Reference

[1]HumanSplat: Generalizable Single-Image Human Gaussian Splatting with Structure Priors

[2]SV3D: Novel Multi-view Synthesis and 3D Generation from a Single Image Using Latent Video Diffusion

[3]Taming Transformers for High-Resolution Image Synthesis

[4]Stable Video Diffusion: Scaling Latent Video Diffusion Models to Large Datasets

[5]普吕克坐标 Plücker coordinates 表示直线