GaussianCube-论文笔记

GaussianCube: A Structured and Explicit Radiance Representation for 3D Gener

项目地址

NeurlPS 2024

Fig. 1: Overview

Abstract

我们引入了一种既结构化又完全显式的辐射表示法，从而极大地促进了 3D 生成模型。现有的辐射表示要么需要隐式特征解码器，降低了表示的建模能力；要么在空间上是非结构化的，因此很难与主流的 3D 扩散方法集成。我们的 GaussianCube 使用一种新颖的密度约束高斯拟合算法，该算法使用固定数量的自由高斯函数实现高精度拟合，然后通过 Optimal Transport 将这些高斯重新排列到预定义的体素网格中。由于 GaussianCube 是一种结构化网格表示法，因此我们可以使用标准 3D U-Net 作为扩散模型的 backbone。更重要的是，高斯函数的高精度拟合使我们能够以比以往的结构化表示少一个到两个数量级的参数，实现高质量的表示。GaussianCube 的紧凑性大大降低了 3D 生成模型的难度。我们在无条件和类条件物体生成、数字人创建和 text-to-3D 合成方面进行了广泛实验，结果表明，我们的模型在质量和量化指标上都取得了 SOTA 的生成结果，突显了 GaussianCube 作为一种高度精确且多功能的辐射表示在 3D 生成模型中的潜力。

Intruduction

大多数现有 3D 生成模型使用 NeRF 的变体作为 3D 表示，其通常结合显式的结构化代理表示和隐式特征解码器。然而，这些混合 NeRF 变体在生成模型中表现出较弱的表示能力，尤其是在所有对象共享一个隐式解码器时。此外，体渲染的高计算复杂性导致渲染速度慢且内存消耗大。

GaussianCube 是一种结构化且显式的辐射表示法，具备强大的拟合能力。该方法首先通过高斯拟合确保高精度，然后使用 Optimal Transport 将高斯分布在结构化的体素网格中。这种结构化的显式表示允许使用标准的 3D 卷积架构 (如U-Net) 进行扩散建模，避免了复杂的网络设计。GaussianCube 不仅保留了高斯拟合的精度，还减少了模型参数量级，大大降低了生成建模的难度，同时提高了性能。

Method

Fig. 2: Pipeline

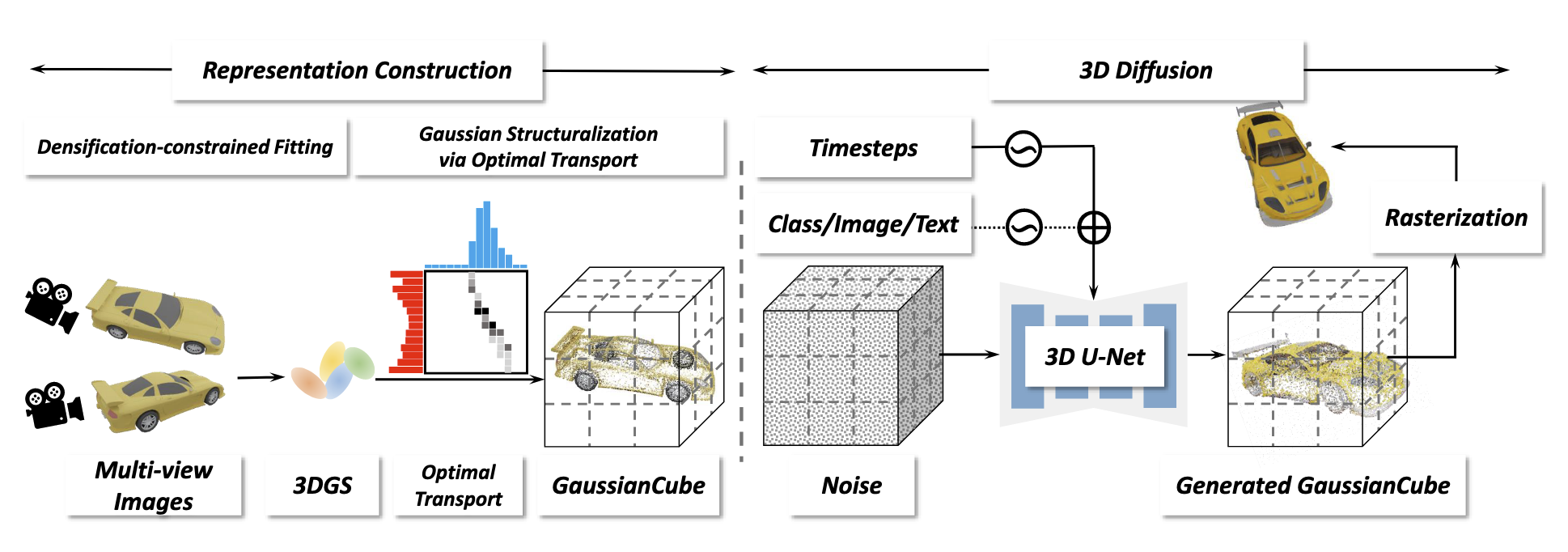
整个 Pipeline 可以分为两个阶段，模型重建和扩散模型。在第一阶段，重建出高斯核数量有限制的高斯模型；第二阶段用 Optimal Transport 将重建出了模型分布在结构化的体素网格中，这个体素网格就是 GaussianCube。

Representation Construction

和 3DGS 一样，每个高斯核 $\boldsymbol{g}_i$ 可以定义为由 $C$ 通道的特征向量 $\boldsymbol{\theta}_i=\left\{\boldsymbol{\mu}_i, \boldsymbol{s}_i, \boldsymbol{q}_i, \alpha_i, \boldsymbol{c}_i\right\} \in \mathbb{R}^C$。

• $\boldsymbol{\mu}\in\R^3$ 表示高斯核的中心位置
• $\boldsymbol{s}\in\R^3$ 表示缩放向量
• $\boldsymbol{q}\in\R^4$ 表示旋转四元数
• $\alpha\in\R$ 表示不透明度
• $\boldsymbol{c}\in\R^3$ 表示颜色特征向量

Densification-constrained fitting

这个方法的目的是为了限制不同物体重建出来的高斯核 $\boldsymbol{g}\in\R^{N_{max}\times C}$ 的数量。

Fig. 3: Illustration of representation construction

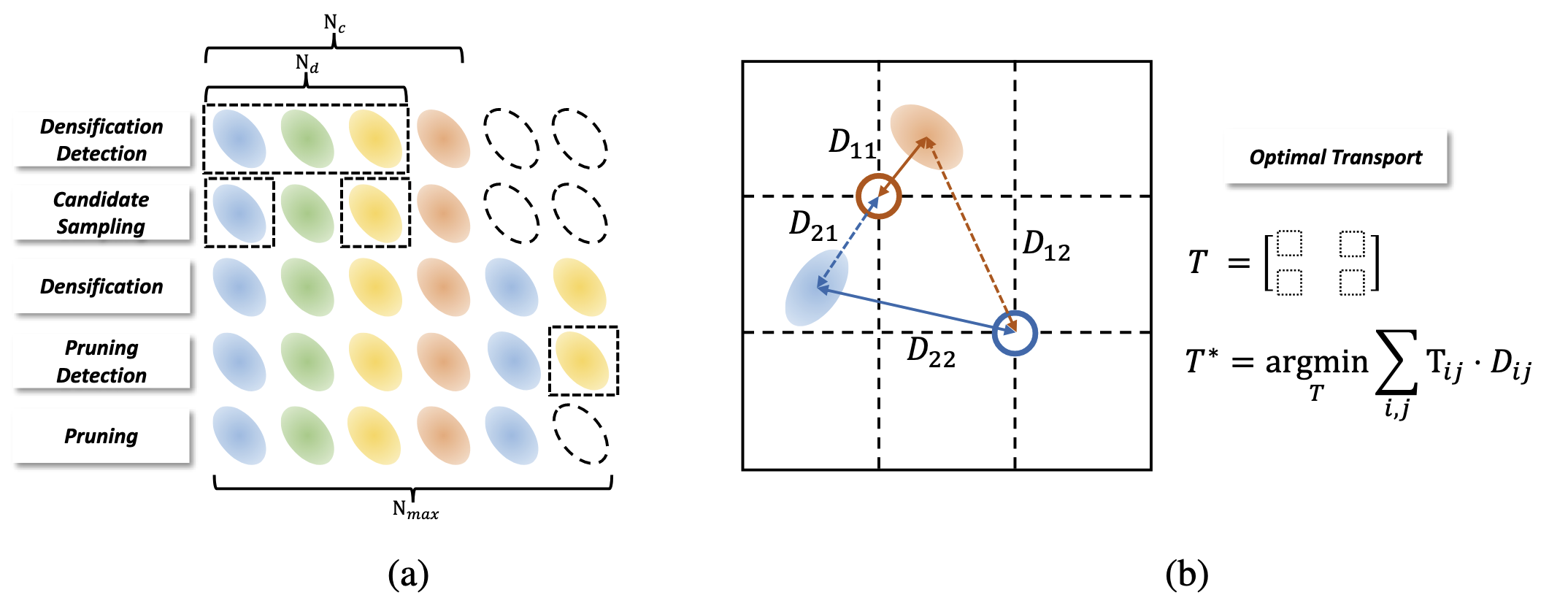
在保留 3DGS 自适应密度控制策略中的 pruning 过程并在 densification 阶段增加了新的约束 (如图 3a 所示)，包含几个独立的阶段：

• Densification Detection：假设当前迭代有 $N_c$ 个高斯核，将 view-space 中位置梯度大于阈值 $\tau$ 的高斯核当作 densification candidates，个数为 $N_d$。
• Candidate sampling：为了防止高斯核的个数超过最大值 $N_{max}$，在 candidates 中挑选 $\min(N_{max}-N_c,N_d)$ 个梯度最大的高斯核。
• Densification：将致密化方法中的 clone 和 split 之间从原来的交替进行修改为单独的步骤。
• Pruning Detection and Pruning：删除那些 $\alpha$ 小于阈值的高斯核。在完成重建后，填充一些 $\alpha=0$ 的高斯核使高斯核的数量达到 $N_{max}$。

Gaussian structuralization via Optimal Transport.

Optimal Transport (OT) 就是让高斯核移动到每个体素的中心位置，并且保留原本的几何关系。预定义一个体素网格 $\boldsymbol{v}\in\R^{N_v\times N_v \times N_v \times C}$，其中 $N_v=\sqrt[3]{N_{max}}$。用 Jonker-Volgenant 算法来计算全局最小传输距离：

$$\underset{\mathbf{T}}{\arg \min } \sum_{i=1}^{N_{max}} \sum_{j=1}^{N_{max}} \mathbf{T}_{ij}\mathbf{D}_{ij} \tag{1}$$

• $\{\boldsymbol{\mu}_i,i=1,...,N_{max}\}$ 表示高斯核的空间位置
• $\{\boldsymbol{x}_i,i=1,...,N_{max}\}$ 表示体素的中心位置
• $\mathbf{D}_{ij}=||\boldsymbol{\mu}_i-\boldsymbol{x}_j||^2$ 表示从 $\boldsymbol{\mu}_i$ 到 $\boldsymbol{x}_j$ 需要移动的距离
• $\mathbf{T} \in \R^{N_{max}\times N_{max}}$ 表示 OT 方案，$\mathbf{T}_{ij}$ 是一个二进制变量表示高斯核 $\boldsymbol{\mu}_i$ 是否移动到 $\boldsymbol{x}_j$。

OT 问题有个约束条件，每个高斯核只能移动到一个体素内，每个体素内只能有一个高斯核。

为什么不直接用最近邻点算法？因为最近邻点算法只关心局部最近，而 Jonker-Volgenant 算法是全局最优，这样能保持整体几何关系的前提下，找到最小的移动距离。

3D Diffusion on GaussianCube

Model architecture

本文只是用 diffusion 中的标准 U-Net，把原本的 2D 算子改成了 3D 算子，并没有做什么复杂的设计。

Conditioning mechanism

对于类条件 (class-conditioned) 扩散模型，用 adaptive group normalization (AdaGN) 把类标签注射到模型内。对于图像条件数字人创建，用一个预训练的 ViT 把条件图像 encode 成 feature tokens 序列。随后，采用交叉注意力机制的方法，让模型学习 3D activations 与 2D 图像 feature tokens 之间的对应关系。在根据文本创建 3D 对象时，也将交叉注意机制作为条件机制，这与之前的文本到图像扩散模型类似。

Training objective

在 3D diffusion 训练中，参数化模型 $\hat{\boldsymbol{y}_\theta}$ 来预测没有噪声的输入 $\boldsymbol{y}_0$：

$$\mathcal{L}_{\text {simple }}=\mathbb{E}_{t, \boldsymbol{y}_0, \boldsymbol{\epsilon}}\left[\left\|\hat{\boldsymbol{y}}_\theta\left(\alpha_t \boldsymbol{y}_0+\sigma_t \boldsymbol{\epsilon}, t, \boldsymbol{c}_{\mathrm{cls}}\right)-\boldsymbol{y}_0\right\|_2^2\right] \tag{2}$$

• $t\in[0,T]$ 表示某一个时间步
• $\boldsymbol{\epsilon}\in\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$ 表示添加的高斯噪声
• $\alpha_t \boldsymbol{y}_0+\sigma_t \boldsymbol{\epsilon}$ 表示输入给模型的带噪声的数据
• $\boldsymbol{c}_{\mathrm{cls}}$ 表示条件信号，只有在训练条件扩散模型的时候才需要

为了提升渲染质量，还加了一个 image-level 的监督：

$$\mathcal{L}_{\text {image }}=\mathbb{E}_{t, I_{\text {pred }}}\left(\sum_l\left\|\Psi^l\left(I_{\text {pred }}\right)-\Psi^l\left(I_{\mathrm{gt}}\right)\right\|_2^2\right)+\mathbb{E}_{t, I_{\mathrm{pred}}}\left(\left\|I_{\mathrm{pred}}-I_{\mathrm{gt}}\right\|_2\right) \tag{3}$$

• $I_{pred}$ 和 $I_{gt}$ 分别表示渲染图片和 GT
• $\Psi^l$ 表示从预训练的 VGG 模型中提取的多分辨率的特征

最后总的损失函数为：

$$\mathcal{L}=\mathcal{L}_{simple}+\lambda\mathcal{L}_{image} \tag{4}$$

Reference

[1]GaussianCube: A Structured and Explicit Radiance Representation for 3D Gener

[2]Diffusion Models Beat GANs on Image Synthesis

[3]Emerging Properties in Self-Supervised Vision Transformers

[4]Large-Vocabulary 3D Diffusion Model with Transformer

[5]High-Resolution Image Synthesis with Latent Diffusion Models